Question
A circle touches the $$x$$-axis and also touches the circle with centre at $$\left( {0,\,3} \right)$$ and radius $$2$$. The locus of the centre of the circle is-
A.
an ellipse
B.
a circle
C.
a hyperbola
D.
a parabola
Answer :
a parabola
Solution :
Equation of circle with centre $$\left( {0,\,3} \right)$$ and radius $$2$$ is $${x^2} + {\left( {y - 3} \right)^2} = 4$$
Let locus of the variable circle is $$\left( {\alpha ,\,\beta } \right)$$
$$\because $$ It touches $$x$$-axis.
$$\therefore $$ It's equation is $${\left( {x - \alpha } \right)^2} + {\left( {y + \beta } \right)^2} = {\beta ^2}$$
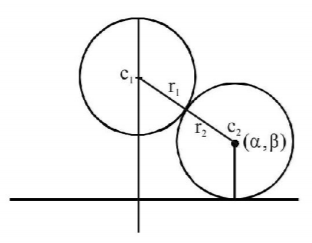
Circle touch externally $$ \Rightarrow {c_1}{c_2} = {r_1} + {r_2}$$
$$\eqalign{ & \therefore \sqrt {{\alpha ^2} + {{\left( {\beta - 3} \right)}^2}} = 2 + \beta \cr & {\alpha ^2} + {\left( {\beta - 3} \right)^2} = {\beta ^2} + 4 + 4\beta \cr & \Rightarrow {\alpha ^2} = 10\left( {\beta - \frac{1}{2}} \right) \cr} $$
$$\therefore $$ Locus is $${x^2} = 10\left( {y - \frac{1}{2}} \right)$$ which is a parabola.
Equation of circle with centre $$\left( {0,\,3} \right)$$ and radius $$2$$ is $${x^2} + {\left( {y - 3} \right)^2} = 4$$
Let locus of the variable circle is $$\left( {\alpha ,\,\beta } \right)$$
$$\because $$ It touches $$x$$-axis.
$$\therefore $$ It's equation is $${\left( {x - \alpha } \right)^2} + {\left( {y + \beta } \right)^2} = {\beta ^2}$$

Circle touch externally $$ \Rightarrow {c_1}{c_2} = {r_1} + {r_2}$$
$$\eqalign{ & \therefore \sqrt {{\alpha ^2} + {{\left( {\beta - 3} \right)}^2}} = 2 + \beta \cr & {\alpha ^2} + {\left( {\beta - 3} \right)^2} = {\beta ^2} + 4 + 4\beta \cr & \Rightarrow {\alpha ^2} = 10\left( {\beta - \frac{1}{2}} \right) \cr} $$
$$\therefore $$ Locus is $${x^2} = 10\left( {y - \frac{1}{2}} \right)$$ which is a parabola.