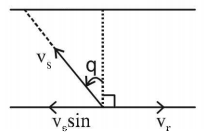
171. The stream of a river is flowing with a speed of $$2\,km/h.$$ A swimmer can swim at a speed of $$4\,km/h.$$ What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
A
$${90^ \circ }$$
B
$${150^ \circ }$$
C
$${120^ \circ }$$
D
$${60^ \circ }$$
Answer :
$${120^ \circ }$$
172. A particle of mass $$m$$ is at rest at the origin at time $$t=0.$$ It is subjected to a force $$F\left( t \right) = {F_0}{e^{ - bt}}$$ in the $$x$$ direction. Its speed $$v\left( t \right)$$ is depicted by which of the following curves?
A
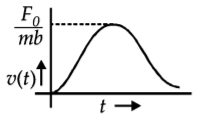

B
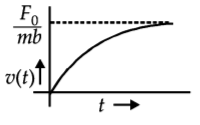

C
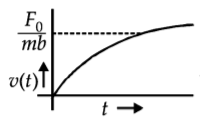

D
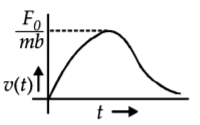

Answer :


173. If the resultant of the vectors $$3\hat i + 4\hat j + 5\hat k$$ and $$5\hat i + 3\hat j + 4\hat k$$ makes an angle $$\theta $$ with $$x$$-axis, then $$\cos \theta $$ is
A
$$0.07$$
B
$$0.574$$
C
$$0.111$$
D
$$0.123$$
Answer :
$$0.574$$
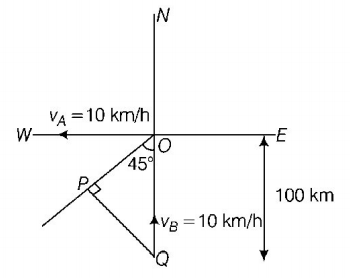
174. A ship $$A$$ is moving Westwards with a speed of $$10\,km\,{h^{ - 1}}$$ and a ship $$B$$ $$100\,km$$ South of $$A,$$ is moving Northwards with a speed of $$10\,km\,{h^{ - 1}}.$$ The time after which the distance between them becomes shortest is
A
$$0\,h$$
B
$$5\,h$$
C
$$5\sqrt 2 \,h$$
D
$$10\sqrt 2 \,h$$
Answer :
$$5\,h$$
175. The position vector of a particle is $$r = \left( {a\cos \omega t} \right)\hat i + \left( {a\sin \omega t} \right)\hat j.$$ The velocity of the particle is
A
directed towards the origin
B
directed away from the origin
C
parallel to the position vector
D
perpendicular to the position vector
Answer :
perpendicular to the position vector
176. A stone tied to the end of a string of $$1\,m$$ long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revolutions in $$44\,s,$$ what is the magnitude and direction of acceleration of the stone?
A
$$\frac{\pi }{4}m{s^{ - 2}}$$ and direction along the radius towards the centre
B
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius away from centre
C
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre
D
$${\pi ^2}m{s^{ - 2}}$$ and direction along the tangent to the
circle
Answer :
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre
177.
Which of the following graphs gives the equation
$$x = {v_0}t + \frac{1}{2}a{t^2}$$
A
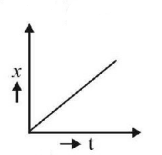

B
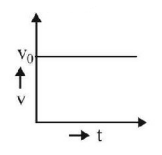

C
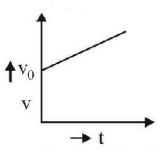

D
None of these
Answer :


178. If distance covered by a particle is zero, what can you say about its displacement?
A
It may or may not be zero
B
It cannot be zero
C
It is negative
D
It must be zero
Answer :
It must be zero
179. The range of a projectile is $$R$$ when the angle of projection is $${40^ \circ }.$$ For the same velocity of projection and range, the other possible angle of projection is
A
$${45^ \circ }$$
B
$${50^ \circ }$$
C
$${60^ \circ }$$
D
$${40^ \circ }$$
Answer :
$${50^ \circ }$$
180. The equation of trajectory of projectile is given by $$y = \frac{x}{{\sqrt 3 }} - \frac{{g{x^2}}}{{20}},$$ where $$x$$ and $$y$$ are in metre. The maximum range of the projectile is
A
$$\frac{8}{3}m$$
B
$$\frac{4}{3}m$$
C
$$\frac{3}{4}m$$
D
$$\frac{3}{8}m$$
Answer :
$$\frac{4}{3}m$$