141. A particle experiences constant acceleration for $$20$$ seconds after starting from rest. If it travels a distance $${s_1}$$ in the first $$10$$ seconds and distance $${s_2}$$ in the next $$10$$ seconds, then
A
$${s_2} = {s_1}$$
B
$${s_2} = 2{s_1}$$
C
$${s_2} = 3{s_1}$$
D
$${s_2} = 4{s_1}$$
Answer :
$${s_2} = 3{s_1}$$
142. A body is moving with velocity $$30\,m/s$$ towards East. After $$10s,$$ its velocity becomes $$40\,m/s$$ towards North. The average acceleration of the body is
A
$$7\,m/{s^2}$$
B
$$\sqrt 7 \,m/{s^2}$$
C
$$5\,m/{s^2}$$
D
$$1\,m/{s^2}$$
Answer :
$$5\,m/{s^2}$$
143. A water fountain on the ground sprinkles water all around it. If the speed of water coming out of the fountain is $$v,$$ the total area around the fountain that gets wet is :
A
$$\pi \frac{{{v^4}}}{{{g^2}}}$$
B
$$\frac{\pi }{2}\frac{{{v^4}}}{{{g^2}}}$$
C
$$\pi \frac{{{v^2}}}{{{g^2}}}$$
D
$$\pi \frac{{{v^2}}}{g}$$
Answer :
$$\pi \frac{{{v^4}}}{{{g^2}}}$$
144. A body of mass $$m$$ is projected horizontally with a velocity $$v$$ from the top of a tower of height $$h$$ and it reaches the ground at a distance $$x$$ from the foot of the tower. If a second body of mass $$2m$$ is projected horizontally from the top of a tower of height $$2h,$$ it reaches the ground at a distance $$2x$$ from the foot of the tower. The horizontal velocity of the second body is
A
$$v$$
B
$$2v$$
C
$$\sqrt {2v} $$
D
$$\frac{v}{2}$$
Answer :
$$\sqrt {2v} $$
145. Two balls $$A$$ and $$B$$ of same mass are thrown from the top of the building. A thrown upward with velocity $$v$$ and $$B,$$ thrown down with velocity $$v,$$ then
A
velocity $$A$$ is more than $$B$$ at the ground
B
velocity of $$B$$ is more than $$A$$ at the ground
C
both $$A\,\& \,B$$ strike the ground with same velocity
D
None of these
Answer :
both $$A\,\& \,B$$ strike the ground with same velocity
146.
For an observer on trolley direction of projection of particle is shown in the figure, while for observer on ground ball rise vertically. The maximum height reached by ball from trolley is
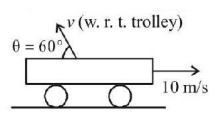
A
$$10\,m$$
B
$$15\,m$$
C
$$20\,m$$
D
$$5\,m$$
Answer :
$$15\,m$$
147. A body moves in straight line with velocity $${v_1}$$ for $${\frac{1}{3}^{rd}}$$ time and for remaining time with $${v_2}.$$ Find average velocity.
A
$$\frac{{{v_1}}}{3} + \frac{{2{v_2}}}{3}$$
B
$$\frac{{{v_1}}}{3} + \frac{{{v_2}}}{3}$$
C
$$\frac{{2{v_1}}}{3} + \frac{{{v_2}}}{3}$$
D
$${v_1} + \frac{{2{v_2}}}{3}$$
Answer :
$$\frac{{{v_1}}}{3} + \frac{{2{v_2}}}{3}$$
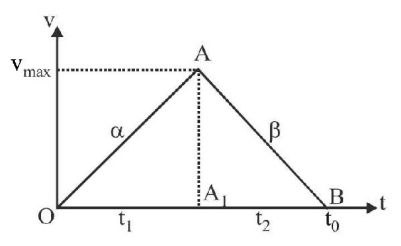
148. A car accelerates from rest at a constant rate $$\alpha $$ for some time, after which it decelerates at a constant rate $$\beta $$ and comes to rest. If the total time elapsed is $$t,$$ then the maximum velocity acquired by the car is
A
$$\left( {\frac{{{\alpha ^2} + {\beta ^2}}}{{\alpha \beta }}} \right)t$$
B
$$\left( {\frac{{{\alpha ^2} - {\beta ^2}}}{{\alpha \beta }}} \right)$$
C
$$\frac{{\left( {\alpha + \beta } \right)t}}{{\alpha \beta }}$$
D
$$\frac{{\alpha \beta t}}{{\alpha + \beta }}$$
Answer :
$$\frac{{\alpha \beta t}}{{\alpha + \beta }}$$
149. A projectile is fired from the surface of the earth with a velocity of $$5\,m{s^{ - 1}}$$ and angle $$\theta $$ with the horizontal. Another projectile fired from another planet with a velocity of $$3\,m{s^{ - 1}}$$ at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is (in $$m{s^{ - 2}}$$ ) given $$g = 9.8\,m/{s^2}$$
A
3.5
B
5.9
C
16.3
D
110.8
Answer :
3.5
150. Two pegs $$A$$ and $$B$$ thrown with speeds in the ratio $$1:3$$ acquired the same heights. If $$A$$ is thrown at an angle of $${30^ \circ }$$ with the horizontal, the angle of projection of $$B$$ will be
A
$${0^ \circ }$$
B
$${\sin ^{ - 1}}\left( {\frac{1}{8}} \right)$$
C
$${\sin ^{ - 1}}\left( {\frac{1}{6}} \right)$$
D
$${\sin ^{ - 1}}\left( {\frac{1}{2}} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\frac{1}{6}} \right)$$