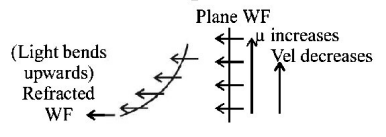
41. On a hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens' principle leads us to conclude that as it travels, the light beam :
A
bends downwards
B
bends upwards
C
becomes narrower
D
goes horizontally without any deflection
Answer :
bends upwards
42.
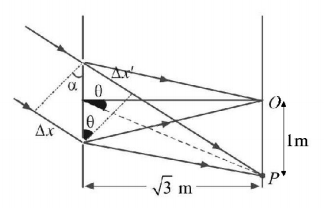
The $$YDSE$$ apparatus is as shown in Fig. The condition for point $$P$$ to be a dark fringe is
A
$$\left( {{l_1} - {l_3}} \right) + \left( {{l_2} - {l_4}} \right) = n\lambda $$
B
$$\left( {{l_1} - {l_2}} \right) + \left( {{l_3} - {l_4}} \right) = \frac{{\left( {2n - 1} \right)}}{2}\lambda $$
C
$$\left( {{l_1} - {l_3}} \right) + \left( {{l_2} - {l_4}} \right) = \frac{{\left( {2n - 1} \right)\lambda }}{2}$$
D
$$\left( {{l_1} - {l_2}} \right) + \left( {{l_4} - {l_3}} \right) = \frac{{\left( {2n - 1} \right)\lambda }}{2}$$
Answer :
$$\left( {{l_1} - {l_2}} \right) + \left( {{l_3} - {l_4}} \right) = \frac{{\left( {2n - 1} \right)}}{2}\lambda $$
43.
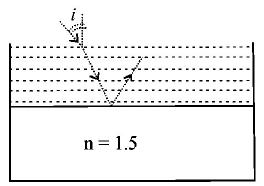
Consider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index $$\mu .$$ A student finds that, irrespective of what the incident angle $$i$$ (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of $$\mu $$ is :
A
$$\sqrt {\frac{5}{3}} $$
B
$$\frac{3}{{\sqrt 5 }}$$
C
$$\frac{5}{{\sqrt 3 }}$$
D
$$\frac{4}{3}$$
Answer :
$$\frac{3}{{\sqrt 5 }}$$
44. When an unpolarized light of intensity $${I_0}$$ is incident on a polarizing sheet, the intensity of the light which does not get transmitted is
A
$$\frac{1}{4}{I_0}$$
B
$$\frac{1}{2}{I_0}$$
C
$${I_0}$$
D
zero
Answer :
$$\frac{1}{2}{I_0}$$
45.
This question has a paragraph followed by two statements, Statement - 1 and Statement - 2. Of the given four alternatives after the statements, choose the one that describes the statements.
A thin air film is formed by putting the convex surface of a plane-convex lens over a plane glass plate. With monochromatic light, this film gives an interference pattern due to light reflected from the top (convex) surface and the bottom (glass plate) surface of the film.
Statement - 1 : When light reflects from the air-glass plate interface, the reflected wave suffers a phase change of $$\pi .$$
Statement - 2 : The centre of the interference pattern is
dark.
A
Statement - 1 is true, Statement - 2 is true, Statement - 2 is the correct explanation of Statement - 1.
B
Statement - 1 is true, Statement - 2 is true, Statement - 2 is not the correct explanation of Statement - 1.
C
Statement - 1 is false, Statement - 2 is true.
D
Statement - 1 is true, Statement - 2 is false.
Answer :
Statement - 1 is true, Statement - 2 is true, Statement - 2 is not the correct explanation of Statement - 1.
46. From a medium of index of refraction $${{n_1}},$$ monochromatic light of wavelength $$\lambda $$ is incident normally on a thin film of uniform thickness $$L$$ (where $$L > 0.1\lambda $$ ) and index of refraction $${{n_2}}.$$ The light transmitted by the film travels into a medium with refractive index $${{n_3}}.$$ The value of minimum film thickness when maximum light is transmitted if $$\left( {{n_1} < {n_2} < {n_3}} \right)$$ is
A
$$\frac{{{n_1}\lambda }}{{2{n_2}}}$$
B
$$\frac{{{n_1}\lambda }}{{4{n_2}}}$$
C
$$\frac{\lambda }{{4{n_2}}}$$
D
$$\frac{\lambda }{{2{n_2}}}$$
Answer :
$$\frac{{{n_1}\lambda }}{{4{n_2}}}$$
47. If $${I_0}$$ is the intensity of the principal maximum in the single slit diffraction pattern, then what will be its intensity when the slit width is doubled?
A
$$4\,{I_0}$$
B
$$2\,{I_0}$$
C
$$\frac{{{I_0}}}{2}$$
D
$${I_0}$$
Answer :
$$4\,{I_0}$$
48.
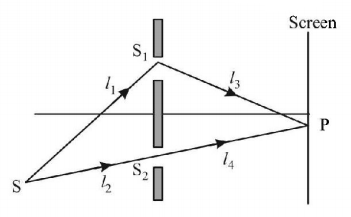
A parallel beam of light $$\left( {\lambda = 5000\,\mathop {\text{A}}\limits^ \circ } \right)$$ is incident at an angle $$\alpha = {30^ \circ }$$ with the normal to the slit plane in $$YDSE.$$ Assume that the intensity due to each slit at any point on the screen is $${I_0}.$$ Point $$O$$ is equidistant from $${S_1}$$ and $${S_2}.$$ The distance between slit is $$1\,mm,$$ then the intensity at
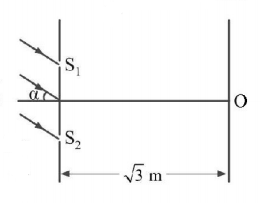
A
$$O$$ is $$3\,{I_0}$$
B
$$O$$ is zero
C
a point $$1\,m$$ below $$O$$ is $$4\,{I_0}$$
D
a point in the screen $$1\,m$$ below $$O$$ is zero
Answer :
a point $$1\,m$$ below $$O$$ is $$4\,{I_0}$$
49. Two beams, $$A$$ and $$B,$$ of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam $$A$$ has maximum intensity (and beam $$B$$ has zero intensity), a rotation of polaroid through $${30^ \circ }$$ makes the two beams appear equally bright. If the initial intensities of the two beams are $${I_A}$$ and $${I_B}$$ respectively, then $$\frac{{{I_A}}}{{{I_B}}}$$ equals
A
3
B
$$\frac{3}{2}$$
C
1
D
$$\frac{1}{3}$$
Answer :
$$\frac{1}{3}$$
50. When a plastic thin film of refractive index 1.45 is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes. The thickness of the film, if the wavelength of light is $$5890\,\mathop {\text{A}}\limits^ \circ ,$$ will be
A
$$6.544 \times {10^{ - 4}}cm$$
B
$$6.544 \times {10^{ - 4}}m$$
C
$$6.54 \times {10^{ - 4}}cm$$
D
$$6.5 \times {10^{ - 4}}cm$$
Answer :
$$6.544 \times {10^{ - 4}}cm$$