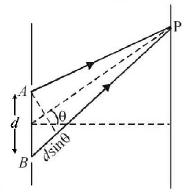
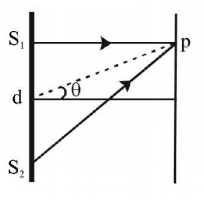
111. In Young’s double slit experiment intensity at a point is $$\left( {\frac{1}{4}} \right)$$ of the maximum intensity. Angular position of this point is
A
$${\sin ^{ - 1}}\left( {\frac{\lambda }{{d}}} \right)$$
B
$${\sin ^{ - 1}}\left( {\frac{\lambda }{{2\,d}}} \right)$$
C
$${\sin ^{ - 1}}\left( {\frac{\lambda }{{3\,d}}} \right)$$
D
$${\sin ^{ - 1}}\left( {\frac{\lambda }{{4\,d}}} \right)$$
Answer :
$${\sin ^{ - 1}}\left( {\frac{\lambda }{{3\,d}}} \right)$$
112. A polaroid is placed at $${45^ \circ }$$ to an incoming light of intensity $$I.$$ Now the intensity of light after polarisation would be
A
$$I$$
B
$$\frac{I}{2}$$
C
$$\frac{I}{{\sqrt 2 }}$$
D
zero
Answer :
$$\frac{I}{2}$$
113. In a Young’s double slit experiment, the fringes are displaced by a distance $$x$$ when a glass plate of refractive index $$1.5$$ is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is $$\left( {\frac{3}{2}} \right)x.$$ The refractive index of second plate is
A
1.75
B
1.50
C
1.25
D
1.00
Answer :
1.75
114.
A double slit, $${S_1} - {S_2}$$ is illuminated by a light source $$S$$ emitting light of wavelength $$\lambda .$$ The slits are separated by a distance $$d.$$ A plane mirror is placed at a distance $$D$$ in front of the slits and a screen is placed at a distance $$2D$$ behind the slits. The screen receives light reflected only by the plane mirror. The fringe-width of the interference pattern on the screen is

A
$$\frac{{D\lambda }}{d}$$
B
$$\frac{{2D\lambda }}{d}$$
C
$$\frac{{3D\lambda }}{d}$$
D
$$\frac{{4D\lambda }}{d}$$
Answer :
$$\frac{{4D\lambda }}{d}$$
115. In young's double - slit experiment, the separation between the slits is $$d,$$ distance between the slit and screen is $$D\left( {D > > D} \right).$$ In the interference pattern, there is a maxima exactly in front of each slit. Then the possible wavelength(s) used. in the experiment are
A
$$\frac{{{d^2}}}{D},\frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{3D}}$$
B
$$\frac{{{d^2}}}{D},\frac{{{d^2}}}{{3D}},\frac{{{d^2}}}{{5D}}$$
C
$$\frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{4D}},\frac{{{d^2}}}{{6D}}$$
D
None of these
Answer :
$$\frac{{{d^2}}}{{2D}},\frac{{{d^2}}}{{4D}},\frac{{{d^2}}}{{6D}}$$