21. In Young's double slit experiment, one of the slit is wider than other, so that amplitude of the light from one slit is double of that from other slit. If $${I_m}$$ be the maximum intensity, the resultant intensity $$I$$ when they interfere at phase difference $$\phi $$ is given by:
A
$$\frac{{{I_m}}}{9}\left( {4 + 5\,\cos \phi } \right)$$
B
$$\frac{{{I_m}}}{3}\left( {1 + 2\,{{\cos }^2}\frac{\phi }{2}} \right)$$
C
$$\frac{{{I_m}}}{5}\left( {1 + 4\,{{\cos }^2}\frac{\phi }{2}} \right)$$
D
$$\frac{{{I_m}}}{9}\left( {1 + 8\,{{\cos }^2}\frac{\phi }{2}} \right)$$
Answer :
$$\frac{{{I_m}}}{9}\left( {1 + 8\,{{\cos }^2}\frac{\phi }{2}} \right)$$
22. In Young’s double slit experiment using monochromatic light the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
A
$$38.2\,\mathop {\text{A}}\limits^ \circ $$
B
$$68.32\,\mathop {\text{A}}\limits^ \circ $$
C
$$5892\,\mathop {\text{A}}\limits^ \circ $$
D
$$528.32\,\mathop {\text{A}}\limits^ \circ $$
Answer :
$$5892\,\mathop {\text{A}}\limits^ \circ $$
23. If one of the slits of a standard Young’s double slit experiment is covered by a thin parallel sided glass slab so that it transmits only one half the light intensity of the other, then -
A
the fringe pattern will get shifted towards the covered slit
B
the fringe pattern will get shifted away from the covered slit
C
the bright fringes will become more bright and the dark ones will become less bright
D
the fringe width will changed
Answer :
the fringe pattern will get shifted towards the covered slit
24. Ona hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens' principle leads us to conclude that as it travels, the light beam:
A
bends downwards
B
bends upwards
C
becomes narrower
D
goes horizontally without any deflection
Answer :
bends upwards
25. Two beams of light having intensities $$I$$ and $$4\,I$$ interfere to produce a fringe pattern on a screen. The phase difference between the beams is $${\frac{\pi }{2}}$$ at point $$A$$ and $$\pi $$ at point $$B.$$ Then the difference between the resultant intensities at $$A$$ and $$B$$ is
A
$$2\,I$$
B
$$4\,I$$
C
$$5\,I$$
D
$$7\,I$$
Answer :
$$4\,I$$
26. When the diffraction pattern from a certain slit illuminated with laser light $$\left( {\lambda = 6330\,\mathop {\text{A}}\limits^ \circ } \right)$$ is projected on a screen $$150\,cm$$ from the slit, the second minima on each side are separated by $$8\,cm.$$ This tells us that :
A
the slit is approximately $$0.005\,cm$$ wide
B
the slit is approximately $$0.05\,cm$$ wide
C
$$\frac{a}{\lambda }$$ is approximately $$7.5$$ ($$a$$ is the slit width)
D
$$\frac{a}{\lambda }$$ is approximately $$750$$
Answer :
the slit is approximately $$0.005\,cm$$ wide
27. The box of a pin hole camera, of length $$L,$$ has a hole of radius $$a.$$ It is assumed that when the hole is illuminated by a parallel beam of light of wavelength $$\lambda $$ the spread of the spot (obtained on the opposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction. The spot would then have its minimum size (say $${b_{\min }}$$ ) when :
A
$$a = \sqrt {\lambda \,L} \,{\text{and}}\,{b_{\min }} = \sqrt {4\lambda \,L} $$
B
$$a = \frac{{{\lambda ^2}}}{L}\,{\text{and}}\,{b_{\min }} = \sqrt {4\lambda \,L} $$
C
$$a = \frac{{{\lambda ^2}}}{L}\,{\text{and}}\,{b_{\min }} = \left( {\frac{{2{\lambda ^2}}}{L}} \right)$$
D
$$a = \sqrt {\lambda \,1} \,{\text{and}}\,{b_{\min }} = \left( {\frac{{2{\lambda ^2}}}{L}} \right)$$
Answer :
$$a = \sqrt {\lambda \,L} \,{\text{and}}\,{b_{\min }} = \sqrt {4\lambda \,L} $$
28. A plane wave of monochromatic light falls normally on a uniform thin layer of oil which covers a glass plate. The wavelength of source can be varies continuously. Complete destructive interference is observed for $$\lambda = 5000\,\mathop {\text{A}}\limits^ \circ $$ and $$\lambda = 1000\,\mathop {\text{A}}\limits^ \circ $$ and for no other wavelength in between. If $$\mu $$ of oil is $$1.3$$ and that of glass is $$1.5,$$ the thickness of the film will be
A
$$6.738 \times {10^{ - 5}}cm$$
B
$$5.7 \times {10^{ - 5}}cm$$
C
$$4 \times {10^{ - 5}}cm$$
D
$$2.8 \times {10^{ - 5}}cm$$
Answer :
$$6.738 \times {10^{ - 5}}cm$$
29. A monochromatic light is used in Young's double slit experiment when one of the slits is covered by a transparent sheet of thickness $$1.8\,mm,$$ made of material of refractive index $${\mu _1}$$ number of fringes which shift is 18, when another sheet of thickness $$3.6\,mm,$$ made of material of refractive index $${\mu _2}$$ is used, number of fringes which shift is 9. Relation between $${\mu _1}$$ and $${\mu _2}$$ is given by
A
$$4{\mu _2} - {\mu _1} = 3$$
B
$$4{\mu _1} - {\mu _2} = 3$$
C
$$3{\mu _2} - {\mu _1} = 4$$
D
$$2{\mu _1} - {\mu _2} = 4$$
Answer :
$$4{\mu _2} - {\mu _1} = 3$$
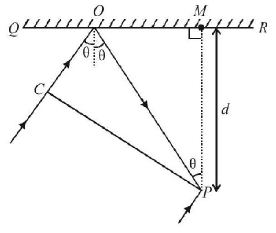
30.
In the adjacent diagram, $$CP$$ represents a wave front and $$AO$$ & $$BP,$$ the corresponding two rays. Find the condition on $$\theta $$ for constructive interference at $$P$$ between the ray $$BP$$ and reflected ray $$OP.$$

A
$$\cos \theta = \frac{{3\,\lambda }}{{2\,d}}$$
B
$$\cos \theta = \frac{{\lambda }}{{4\,d}}$$
C
$$sec\theta - \cos \theta = \frac{\lambda }{d}$$
D
$$sec\theta - \cos \theta = \frac{4\,\lambda }{d}$$
Answer :
$$\cos \theta = \frac{{\lambda }}{{4\,d}}$$