51. In Fresnel's biprism experiment the width of 10 fringes is $$2\,cm$$ which are formed at a distance of 2 meter from the slit. If the wavelength of light is $$5100\,\mathop {\text{A}}\limits^ \circ $$ then the distance between two coherent sources will be
A
$$5.1 \times {10^{ - 4}}\,m$$
B
$$5.1 \times {10^{ 4}}\,cm$$
C
$$5.1 \times {10^{ - 4}}\,mm$$
D
$$10.1 \times {10^{ - 4}}\,cm$$
Answer :
$$5.1 \times {10^{ - 4}}\,m$$
52. The phase difference between incident wave and reflected wave is $${180^ \circ }$$ when light ray
A
enters into glass from air
B
enters into air from glass
C
enters into glass from diamond
D
enters into water from glass
Answer :
enters into glass from air
53.
In figure, Young’s double slit experiment $$Q$$ is the position of the first bright fringe on the right side of $$O.$$ $$P$$ is the 11th fringe on the other side, as measured from $$Q.$$ If $$\lambda = 6000\,\mathop {\text{A}}\limits^ \circ ,$$ then $${S_1}B$$ will be equal to

A
$$6 \times {10^{ - 6}}m$$
B
$$6.6 \times {10^{ - 6}}m$$
C
$$3.318 \times {10^{ - 7}}m$$
D
$$3.144 \times {10^{ - 7}}m$$
Answer :
$$6 \times {10^{ - 6}}m$$
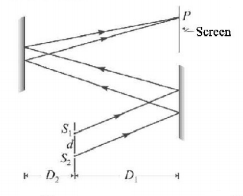
54.
In a double slit experiment slits $${S_1},{S_2}$$ is illuminated by a coherent light of wavelength $$\lambda .$$ The slits are separated by a distance $$d.$$ The experimental set up is modified by using plane mirrors as shown in figure. Find the fringe width of interference pattern on the screen.
A
$$\frac{{\left( {3{D_1} + 2{D_2}} \right)\lambda }}{d}$$
B
$$\frac{{\left( {2{D_1} + 3{D_2}} \right)\lambda }}{d}$$
C
$$\frac{{\left( {3{D_2} - 3{D_1}} \right)\lambda }}{d}$$
D
$$\frac{{\left( {3{D_1} - 2{D_2}} \right)\lambda }}{{2d}}$$
Answer :
$$\frac{{\left( {3{D_1} + 2{D_2}} \right)\lambda }}{d}$$
55. A light wave of wavelength $${\lambda _0}$$, propagates from point $$A$$ to point $$B.$$ We introduce in its path a glass plate of refractive index $$n$$ and thickness $$l.$$ The introduction of the plate alters the phase of the plate at $$B$$ by an angle $$\phi .$$ If $$\lambda $$ is the wavelength of lights on emerging from the plate, then
A
$$\Delta \phi = 0$$
B
$$\Delta \phi = \frac{{2\pi l}}{{{\lambda _0}}}$$
C
$$\Delta \phi = 2\pi {\ln ^2}\left( {\frac{1}{\lambda } - \frac{1}{{{\lambda _0}}}} \right)$$
D
$$\Delta \phi = \frac{{2\pi l}}{{{\lambda _0}}}\left( {n - 1} \right)$$
Answer :
$$\Delta \phi = \frac{{2\pi l}}{{{\lambda _0}}}\left( {n - 1} \right)$$
56. In $$YDSE$$ a light containing two wavelengths $$500\,nm$$ and $$700\,nm$$ are used. Find the minimum distance where maxima of two wavelengths coincide. Given $$\frac{D}{d} = {10^3},$$ where $$D$$ is the distance between the slits and the screen and $$d$$ is the distance between the slits.
A
$$1.2\,m$$
B
$$3.5\,mm$$
C
$$2.8\,mm$$
D
$$8.1\,mm$$
Answer :
$$3.5\,mm$$
57. A beam of unpolarised light of intensity $${{I_0}}$$ is passed through a polaroid $$A$$ and then through another polaroid $$B$$ which is oriented so that its principal plane makes an angle of 45° relative to that of $$A.$$ The intensity of the emergent light is
A
$${{I_0}}$$
B
$$\frac{{{I_0}}}{2}$$
C
$$\frac{{{I_0}}}{4}$$
D
$$\frac{{{I_0}}}{8}$$
Answer :
$$\frac{{{I_0}}}{4}$$
58. In a Young’s double slit experiment, $$12$$ fringes are observed to be formed in a certain segment of the screen when light of wavelength $$600\,nm$$ is used. If the wavelength of light is changed to $$400\,nm,$$ number of fringes observed in the same segment of the screen is given by
A
12
B
18
C
24
D
30
Answer :
18
59. Huygen’s concept of secondary wave
A
allows us to find the focal length of a thick lens
B
is a geometrical method to find a wavefront
C
is used to determine the velocity of light
D
is used to explain polarisation
Answer :
is a geometrical method to find a wavefront
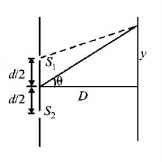
60.
Two coherent point sources $${S_1}$$ and $${S_2}$$ are separated by a small distance $$'d'$$ as shown. The fringes obtained on the screen will be

A
points
B
straight lines
C
semi - circles
D
concentric circles
Answer :
concentric circles