31.
An initially parallel cylindrical beam travels in a medium of refractive index $$\mu \left( I \right) = {\mu _0} + {\mu _2}I,$$ where $${\mu _0}$$ and $${\mu _2}$$ are positive constants and $$I$$ is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
The initial shape of the wave front of the beam is
A
convex
B
concave
C
convex near the axis and concave near the periphery
D
planar
Answer :
planar
32. A beam of light of wave length $$600\,nm$$ from a distance source falls on a single slit $$1mm$$ wide and a resulting diffraction pattern is observed on a screen $$2\,m$$ away. The distance between the first dark fringes on either side of central bright fringe is
A
$$1.2\,cm$$
B
$$1.2\,mm$$
C
$$2.4\,cm$$
D
$$2.4\,mm$$
Answer :
$$2.4\,mm$$
33.
The correct curve between refractive index $$\mu $$ and wavelength $$\lambda $$ will be

A
$$A$$
B
$$D$$
C
$$B$$
D
$$C$$
Answer :
$$A$$
34. In an experiment of single slit diffraction pattern, first minimum for red light coincides with first maximum of some other wavelength, If wavelength of red light is $$6600\,\mathop {\text{A}}\limits^ \circ ,$$ then wavelength of first maximum will be :
A
$$3300\,\mathop {\text{A}}\limits^ \circ $$
B
$$4400\,\mathop {\text{A}}\limits^ \circ $$
C
$$5500\,\mathop {\text{A}}\limits^ \circ $$
D
$$6600\,\mathop {\text{A}}\limits^ \circ $$
Answer :
$$4400\,\mathop {\text{A}}\limits^ \circ $$
35. An unpolarised beam of intensity $${I_0}$$ is incident on a pair of nicols making an angle of $${60^ \circ }$$ with each other. The intensity of light emerging from the pair is
A
$${I_0}$$
B
$$\frac{{{I_0}}}{2}$$
C
$$\frac{{{I_0}}}{4}$$
D
$$\frac{{{I_0}}}{8}$$
Answer :
$$\frac{{{I_0}}}{4}$$
36. Consider Fraunh offer diffraction pattern obtained with a single slit illuminated at normal incidence. At the angular position of the first diffraction minimum the phase difference (in radians) between the wavelets from the opposite edges of the slit is
A
$$\frac{\pi }{4}$$
B
$$\frac{\pi }{2}$$
C
$$2\,\pi $$
D
$$\pi $$
Answer :
$$2\,\pi $$
37.
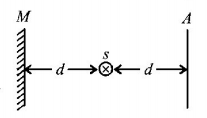
The intensity of a point source of light, $$S,$$ placed at a distance $$d$$ in front of a screen $$A,$$ is $${I_0}$$ at the center of the screen. Find the light intensity at the center of the screen if a completely reflecting plane mirror $$M$$ is placed at a distance $$d$$ behind the source, as shown in figure.
A
$$\frac{{27{I_0}}}{9}$$
B
$$\frac{{25{I_0}}}{9}$$
C
$$\frac{{17{I_0}}}{9}$$
D
$$\frac{{10{I_0}}}{9}$$
Answer :
$$\frac{{10{I_0}}}{9}$$
38. Electromagnetic waves are transverse in nature is evident by
A
polarization
B
interference
C
reflection
D
diffraction
Answer :
polarization
39. The width of the diffraction band varies
A
inversely as the wavelength
B
directly as the width of the slit
C
directly as the distance between the slit and the screen
D
inversely as the size of the source from which the slit is illuminated
Answer :
directly as the distance between the slit and the screen
40.
Two sources $${S_1}$$ and $${S_2}$$ emitting coherent light waves of wavelength $$\lambda $$ in the same phase are situated as shown. The distance $$OP,$$ so that the light intensity detected at $$P$$ is equal to that at $$O$$ is

A
$$D\sqrt 2 $$
B
$$\frac{D}{2}$$
C
$$D\sqrt 3 $$
D
$$\frac{D}{{\sqrt 3 }}$$
Answer :
$$D\sqrt 3 $$