91. A light of wavelength $$6000\,\mathop {\text{A}}\limits^ \circ $$ shines on two narrow slits separated by a distance $$1.0\,mm$$ and illuminates a screen at a distance $$1.5\,m$$ away. When one slit is covered by a thin glass plate of refractive index 1.8 and other slit by a thin glass plate of refractive index $$\mu ,$$ the central maxima shifts by $$0.1\,rad.$$ Both plates have the same thickness of $$0.5\,mm.$$ The value of refractive index $$\mu $$ of the glass is
A
1.4
B
1.5
C
1.6
D
None of these
Answer :
1.6
92. In a Young’s double slit experiment, the two slits act as coherent sources of wave of equal amplitude $$A$$ and wavelength $$\lambda .$$ In another experiment with the same arrangement the two slits are made to act as incoherent sources of waves of same amplitude and wavelength. Ifthe intensity at the middle point of the screen in the first case is $${I_1}$$ and in the second case is $${I_2},$$ then the ratio $$\frac{{{I_1}}}{{{I_2}}}$$ is
A
2
B
1
C
0.5
D
4
Answer :
2
93. A certain region of a soap bubble reflects red light of wavelength $$\lambda = 650\,nm.$$ What is the minimum thickness that this region of the soap bubble could have? Take the index of reflection of the soap film to be $$1.41.$$
A
$$1.2 \times {10^{ - 7}}m$$
B
$$650 \times {10^{ - 9}}m$$
C
$$120 \times {10^{ 7}}m$$
D
$$650 \times {10^{ 5}}m$$
Answer :
$$1.2 \times {10^{ - 7}}m$$
94. A physics professor wants to find the diameter of a human hair by placing it between two flat glass plates, illuminating the plates with light of vacuum wavelength $$\lambda = 552\,nm$$ and counting the number of bright fringes produced along the plates. The Professor find 125 bright fringes between the edge of the plates and the hair. What is the diameter of the hair?
A
$$525 \times {10^{ - 9}}\,m$$
B
$$344 \times {10^{ - 3}}\,m$$
C
$$3.44 \times {10^{ - 5}}\,m$$
D
None of above
Answer :
$$3.44 \times {10^{ - 5}}\,m$$
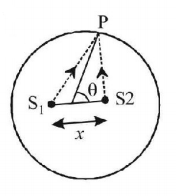
95. Two identical coherent sources are placed on a diameter of a circle of radius $$R$$ at separation $$x\left( { < < R} \right)$$ symmetrical about the center of the circle. The sources emit identical wavelength $$\lambda $$ each. The number of points on the circle of maximum intersity is $$\left( {x = 5\lambda } \right)$$
A
20
B
22
C
24
D
26
Answer :
20
96.
A broad source of light $$\left( {I = 680\,nm} \right)$$ illuminates normally two glass plates $$120\,mm$$ long that touch at one end and are separated by a wire $$0.034\,mm$$ in diameter at the other end. The total number of bright fringes that appear over the $$120\,mm$$ distance is -

A
50
B
100
C
200
D
400
Answer :
100
97. In an experiment, sodium light $$\left( {\lambda = 5890\,\mathop {\text{A}}\limits^ \circ } \right)$$ is employed and interference fringes are obtained in which 20 fringes equally spaced occupy $$2.30\,cm$$ on the screen. When sodium light is replaced by blue light, the setup remaining the same otherwise, 30 fringes occupy $$2.80\,cm.$$ The wavelength of blue light is
A
$$4780\,\mathop {\text{A}}\limits^ \circ $$
B
$$5760\,\mathop {\text{A}}\limits^ \circ $$
C
$$9720\,\mathop {\text{A}}\limits^ \circ $$
D
$$6390\,\mathop {\text{A}}\limits^ \circ $$
Answer :
$$4780\,\mathop {\text{A}}\limits^ \circ $$
98. In a Young’s double slit experiment the intensity at a point where the path difference is $${\frac{\lambda }{6}}$$ ($$\lambda $$ being the wavelength of light used) is $$I.$$ If $${{I_0}}$$ denotes the maximum intensity, $$\frac{I}{{{I_0}}}$$ is equal to
A
$$\frac{3}{4}$$
B
$$\frac{1}{{\sqrt 2 }}$$
C
$$\frac{{\sqrt 3 }}{2}$$
D
$$\frac{1}{2}$$
Answer :
$$\frac{3}{4}$$
99.
A thin slice is cut out of a glass cylinder along a plane parallel to its axis. The slice is placed on a flat glass plate as shown in Figure. The observed interference fringes from this combination shall be

A
straight
B
circular
C
equally spaced
D
having fringe spacing which increases as we go outwards
Answer :
straight
100. The angle of incidence at which reflected light is totally polarized for reflection from air to glass (refractive index $$n$$), is
A
$${\tan ^{ - 1}}\left( {\frac{1}{n}} \right)$$
B
$${\sin ^{ - 1}}\left( {\frac{1}{n}} \right)$$
C
$${\sin ^{ - 1}}(n)$$
D
$${\tan ^{ - 1}}(n)$$
Answer :
$${\tan ^{ - 1}}(n)$$