61. A heavy nucleus having mass number 200 gets disintegrated into two small fragments of mass number 80 and 120. If binding energy per nucleon for parent atom is $$6.5\,MeV$$ and for daughter nuclei is $$7\,MeV$$ and $$8\,MeV$$ respectively, then the energy released in the decay will be -
A
$$200\,MeV$$
B
$$ - 200\,MeV$$
C
$$220\,MeV$$
D
$$180\,MeV$$
Answer :
$$220\,MeV$$
62. An archaeologist analyses the wood in a prehistoric structure and finds that $${C^{14}}$$ (Half life = 5700 years) to $${C^{12}}$$ is only one-fourth of that found in the cells of buried plants. The age of the wood is about
A
5700 years
B
2850 years
C
11,400 years
D
22,800 years
Answer :
11,400 years
63. Half-lives of two radioactive substances $$A$$ and $$B$$ are respectively $$20\,min$$ and $$40\,min.$$ Initially, the samples of $$A$$ and $$B$$ have equal number of nuclei. After $$80\,min$$ the ratio of remaining number of $$A$$ and $$B$$ nuclei is
A
$$1:16$$
B
$$4:1$$
C
$$1:4$$
D
$$1:1$$
Answer :
$$1:4$$
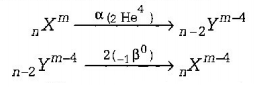
64. A nucleus $$_n{X^m}$$ emits one $$\alpha $$ and two $$\beta $$-particles. The resulting nucleus is
A
$$_n{X^{m - 4}}$$
B
$$_{n - 2}{Y^{m - 4}}$$
C
$$_{n - 4}{Z^{m - 4}}$$
D
None of these
Answer :
$$_n{X^{m - 4}}$$
65. The half life of a radioactive substance is 20 minutes. The approximate time interval $$\left( {{t_2} - {t_1}} \right)$$ between the time $${t_2}$$ when $$\frac{2}{3}$$ of it had decayed and time $${t_1}$$ when $$\frac{1}{3}$$ of it had decayed is :
A
$$14\,min$$
B
$$20\,min$$
C
$$28\,min$$
D
$$7\,min$$
Answer :
$$20\,min$$
66. In gamma ray emission from a nucleus
A
only the proton number changes
B
both the neutron number and the proton number change
C
there is no change in the proton number and the neutron number
D
only the neutron number changes
Answer :
there is no change in the proton number and the neutron number
67. The number of beta particles emitted by a radioactive substance is twice the number of alpha particles emitted by it. The resulting daughter is an
A
isobar of parent
B
isomer of parent
C
isotone of parent
D
isotope of parent
Answer :
isotope of parent
68. A radioactive material decays by simultaneous emission of two particles with respective half-lives 1620 and 810 years. The time, in years, after which one-fourth of the material remains is
A
1080
B
2430
C
3240
D
4860
Answer :
1080
69. The activity of a radioactive sample is measured as $${N_0}$$ counts per minute at $$t = 0$$ and $$\frac{{{N_0}}}{e}$$ counts per minute at $$t = 5\,min.$$ The time (in minute) at which the activity reduces to half its value is
A
$${\log _e}\frac{2}{5}$$
B
$$\frac{5}{{{{\log }_e}2}}$$
C
$$5{\log _{10}}2$$
D
$$5{\log _e}2$$
Answer :
$$5{\log _e}2$$
70. A radioactive nucleus of mass $$M$$ emits a photon of frequency $$\nu $$ and the nucleus recoils. The recoil energy will be
A
$$\frac{{{h^2}{\nu ^2}}}{{2M{c^2}}}$$
B
zero
C
$$h\nu $$
D
$$M{c^2} - h\nu $$
Answer :
$$\frac{{{h^2}{\nu ^2}}}{{2M{c^2}}}$$