161. The half life of radioactive Radon is 3.8 days. The time at the end of which $$\frac{1}{{20}}th$$ of the radon sample will remain undecayed is (given $${\log _{10}}e = 0.4343$$ )
A
3.8 days
B
16.5 days
C
33 days
D
76 days.
Answer :
16.5 days
162. A radioactive sample consists of two distinct species having equal number of atoms initially. The mean life time of one species is $$\tau $$ and that of the other is $$5\tau .$$ The decay products in both cases are stable. A plot is made of the total number of radioactive nuclei as a function of time. Which of the following figures best represent the form of this plot?
A
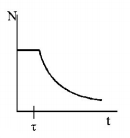

B
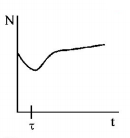

C
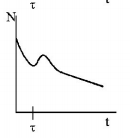

D
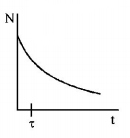

Answer :

