31. Two long parallel wires are at a distance $$2d$$ apart. They carry steady equal currents flowing out of the plane of the paper as shown. The variation of the magnetic field $$B$$ along the line $$XX'$$ is given by
A
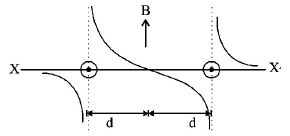

B
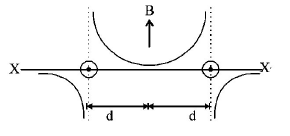

C
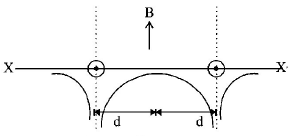

D
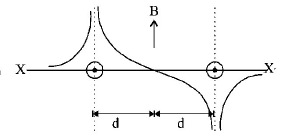

Answer :


32. A uniform magnetic field acts right angles to the direction of motion of electrons. As a result, the electron moves in a circular path of radius $$2\,cm.$$ If the speed of electrons is doubled, then the radius of the circular path will be
A
$$2.0\,cm$$
B
$$0.5\,cm$$
C
$$4.0\,cm$$
D
$$1.0\,cm$$
Answer :
$$4.0\,cm$$
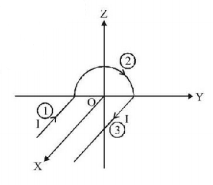
33.
A wire carrying current $$I$$ has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to $$X$$-axis while semicircular portion of radius $$R$$ is lying in $$Y-Z$$ plane. Magnetic field at point $$O$$ is :
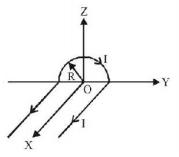
A
$$\overrightarrow B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\mu \hat i \times 2\hat k} \right)$$
B
$$\overrightarrow B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
C
$$\overrightarrow B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i - 2\hat k} \right)$$
D
$$\overrightarrow B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
Answer :
$$\overrightarrow B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
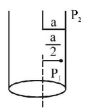
34. A long straight wire of radius $$a$$ carries a steady current $$i.$$ The current is uniformly distributed across its cross section. The ratio of the magnetic field at $$\frac{a}{2}$$ and $$2a$$ is
A
$$\frac{1}{2}$$
B
$$\frac{1}{4}$$
C
4
D
1
Answer :
1
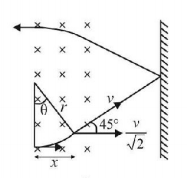
35.
A particle of mass $$m$$ and charge $$q$$ enters a region of magnetic field (as shown) with speed $$v.$$ There is a region in which the magnetic field is absent, as shown. The particle after entering the region collides elastically with a rigid wall. Time after which the velocity of particle becomes antiparallel to its initial velocity is
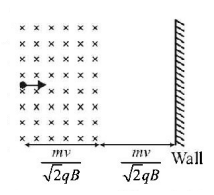
A
$$\frac{m}{{2qB}}\left( {\pi + 4} \right)$$
B
$$\frac{m}{{qB}}\left( {\pi + 2} \right)$$
C
$$\frac{m}{{4qB}}\left( {\pi + 2} \right)$$
D
$$\frac{m}{{4qB}}\left( {2\pi + 3} \right)$$
Answer :
$$\frac{m}{{2qB}}\left( {\pi + 4} \right)$$
36. A galvanometer of resistance $$5\,ohms$$ gives a full scale deflection for a potential difference of $$10\,mV.$$ To convert the galvanometer into a voltmeter giving a full scale deflection for a potential difference of $$1\,V,$$ the size of the resistance that must be attached to the voltmeter is
A
$$0.495\,ohm$$
B
$$49.5\,ohm$$
C
$$495\,ohm$$
D
$$4950\,ohm$$
Answer :
$$495\,ohm$$
37. A current carrying coil is subjected to a uniform magnetic field. The coil will orient so that its plane becomes
A
inclined at $${45^ \circ }$$ to the magnetic field
B
inclined at any arbitrary angle to the magnetic field
C
parallel to the magnetic field
D
perpendicular to magnetic field
Answer :
parallel to the magnetic field
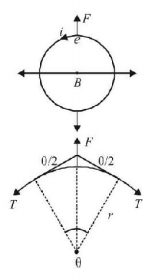
38.
A conducting ring of mass $$2\,kg$$ and radius $$0.5\,m$$ is placed ring on a smooth horizontal plane. The ring carries a current of $$i = 4\,A.$$ A horizontal magnetic field $$B = 10\,T$$ is switched on at time $$t = 0$$ as shown in fig. The initial angular acceleration of the ring will be
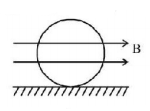
A
$$40\,\pi \,rad\,{s^{ - 2}}$$
B
$$20\,\pi \,rad\,{s^{ - 2}}$$
C
$$5\,\pi \,rad\,{s^{ - 2}}$$
D
$$15\,\pi \,rad\,{s^{ - 2}}$$
Answer :
$$40\,\pi \,rad\,{s^{ - 2}}$$
39.
Two equal electric currents are flowing perpendicular to each other as shown in the figure. $$AB$$ and $$CD$$ are perpendicular to each other and symmetrically placed w.r.t the currents, where do we expect the resultant magnetic field to be zero?
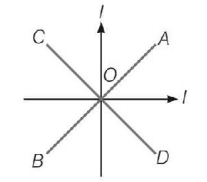
A
On $$AB$$
B
On $$CD$$
C
On both $$AB$$ and $$CD$$
D
On both $$OD$$ and $$BO$$
Answer :
On $$AB$$
40. A conducting loop is placed in a magnetic field of strength $$B$$ perpendicular to its plane. Radius of the loop is $$r,$$ current in the loop is $$i$$ and linear mass density of the wire of loop is $$m.$$ Speed of any transverse wave in the loop will be
A
$$\sqrt {\frac{{Bir}}{m}} $$
B
$$\sqrt {\frac{{Bir}}{{2m}}} $$
C
$$\sqrt {\frac{{2Bir}}{{m}}} $$
D
$$2\sqrt {\frac{{Bir}}{m}} $$
Answer :
$$\sqrt {\frac{{Bir}}{m}} $$