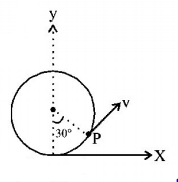
91. A charged particle (charge $$q$$ ) is moving in a circle of radius $$R$$ with uniform speed $$v.$$ The associated magnetic moment $$\mu $$ is given by
A
$$\frac{{qvR}}{2}$$
B
$$qv{R^2}$$
C
$$\frac{{qv{R^2}}}{2}$$
D
$$qvR$$
Answer :
$$\frac{{qvR}}{2}$$
92. A particle of specific charge $$\frac{q}{m} = \pi \,Ck{g^{ - 1}}$$ is projected from the origin towards positive $$x$$-axis with a velocity of $$10\,m{s^{ - 1}}$$ in a uniform magnetic field $$\vec B = - 2\hat k\,T.$$ The velocity $${\vec v}$$ of particle after time $$t = \frac{1}{{12}}s$$ will be (in $$m{s^{ - 1}}$$ )
A
$$5\left[ {\hat i + \sqrt 3 \hat j} \right]$$
B
$$5\left[ {\sqrt 3 \hat i + \hat j} \right]$$
C
$$5\left[ {\sqrt 3 \hat i - \hat j} \right]$$
D
$$5\left[ {\hat i + \hat j} \right]$$
Answer :
$$5\left[ {\sqrt 3 \hat i + \hat j} \right]$$
93.
$$OABC$$ is current carrying square loop an electron is projected from the centre of loop along its diagonal $$AC$$ as shown. Unit vector in the direction of initial acceleration will be

A
$$\hat k$$
B
$$ - \left( {\frac{{\hat i + \hat j}}{{\sqrt 2 }}} \right)$$
C
$$ - \hat k$$
D
$$\frac{{\hat i + \hat j}}{{\sqrt 2 }}$$
Answer :
$$\frac{{\hat i + \hat j}}{{\sqrt 2 }}$$
94. A voltmeter has a range $$0 - V$$ with a series resistance $$R.$$ With a series resistance $$2R,$$ the range is $$0 - V'.$$ The correct relation between $$V$$ and $$V'$$ is
A
$$V' = 2\,V$$
B
$$V' > 2\,V$$
C
$$V' > > 2\,V$$
D
$$V' < 2\,V$$
Answer :
$$V' < 2\,V$$
95. The correct plot of the magnitude of magnetic field $$\overrightarrow B $$ $$vs$$ distance $$r$$ from centre of the wire is, if the radius of wire is $$R$$
A


B


C


D


Answer :


96. Through two parallel wires $$A$$ and $$B,$$ $$10A$$ and $$2A$$ of currents are passed respectively in opposite directions. If the wire $$A$$ is infinitely long and the length of the wire $$B$$ is $$2m,$$ then force on the conductor $$B,$$ which is situated at $$10\,cm$$ distance from $$A,$$ will be
A
$$8 \times {10^{ - 7}}N$$
B
$$8 \times {10^{ - 5}}N$$
C
$$4 \times {10^{ - 7}}N$$
D
$$4 \times {10^{ - 5}}N$$
Answer :
$$8 \times {10^{ - 5}}N$$
97.
The figure shows two infinite semi-cylindrical shells: shell-1 and shell-2. Shell-1 carries current $${i_1},$$ in inward direction normal to the plane of paper, while shell-2 carries same current $${i_1},$$ in opposite direction. A long straight conductor lying along the common axis of the shells is carrying current $${i_2}$$ in direction same as that of current in shell-1. Force per unit length on the wire is

A
zero
B
$$\frac{{{\mu _0}{i_1}{i_2}}}{{2\pi r}}$$
C
$$\frac{{2{\mu _0}{i_1}{i_2}}}{{\pi r}}$$
D
$$\frac{{2{\mu _0}{i_1}{i_2}}}{{{\pi ^2}r}}$$
Answer :
$$\frac{{2{\mu _0}{i_1}{i_2}}}{{{\pi ^2}r}}$$
98. Proton, deuteron and alpha particle of same kinetic energy are moving in circular trajectories in a constant magnetic field. The radii of proton, deuteron and alpha particle are respectively $${r_p},{r_d}$$ and $${r_\alpha }.$$ Which one of the following relation is correct?
A
$${r_\alpha } = {r_p} = {r_d}$$
B
$${r_\alpha } = {r_p} < {r_d}$$
C
$${r_\alpha } > {r_d} > {r_p}$$
D
$${r_\alpha } = {r_d} > {r_p}$$
Answer :
$${r_\alpha } = {r_p} < {r_d}$$
99. A proton, a deuteron and an $$\alpha - $$ particle having the same kinetic energy are moving in circular trajectories in a constant magnetic field. If $${r_p},{r_d},$$ and $${r_\alpha }$$ denote respectively the radii of the trajectories of these particles, then
A
$${r_\alpha } = {r_p} < {r_d}$$
B
$${r_\alpha } > {r_d} > {r_p}$$
C
$${r_\alpha } = {r_d} > {r_p}$$
D
$${r_p} = {r_d} = {r_\alpha }$$
Answer :
$${r_\alpha } = {r_p} < {r_d}$$
100. A straight wire of length $$0.5\,m$$ and carrying a current of $$1.2\,A$$ is placed in uniform magnetic field of induction $$2T.$$ The magnetic field is perpendicular to the length of the wire. The force on the wire is
A
$$2.4\,N$$
B
$$1.2\,N$$
C
$$3.0\,N$$
D
$$2.0\,N$$
Answer :
$$1.2\,N$$