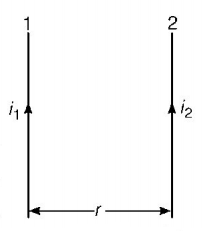
101.
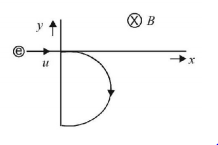
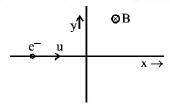
An electron travelling with a speed $$u$$ along the positive $$x$$-axis enters into a region of magnetic field where $$B = - {B_0}\hat k\left( {x > 0} \right).$$ It comes out of the region with speed $$v$$ then
A
$$v = u\,{\text{at}}\,y > 0$$
B
$$v = u\,{\text{at}}\,y < 0$$
C
$$v > u\,{\text{at}}\,y > 0$$
D
$$v > u\,{\text{at}}\,y < 0$$
Answer :
$$v = u\,{\text{at}}\,y < 0$$
102. To convert a galvanometer into an ammeter, one needs to connect a
A
low resistance in parallel
B
high resistance in parallel
C
low resistance in series
D
high resistance in series
Answer :
low resistance in parallel
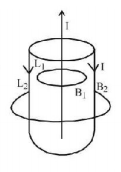
103. A coaxial cable consists of a thin inner conductor fixed along the axis of a hollow outer conductor. The two conductors carry equal currents in opposites directions. Let $${B_1}$$ and $${B_2}$$ be the magnetic fields in the region between the conductors and outside the conductor, respectively Then,
A
$${B_1} \ne 0,{B_2} \ne 0$$
B
$${B_1} = {B_2} = 0$$
C
$${B_1} \ne 0,{B_2} = 0$$
D
$${B_1} = 0,{B_2} \ne 0$$
Answer :
$${B_1} \ne 0,{B_2} = 0$$
104. A particle of charge $$q$$ and mass $$m$$ moves in a circular orbit of radius $$r$$ with angular speed $$\omega .$$ The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
A
$$\omega $$ and $$q$$
B
$$\omega ,$$ $$q$$ and $$m$$
C
$$q$$ and $$m$$
D
$$\omega $$ and $$m$$
Answer :
$$q$$ and $$m$$
105. The magnetic field at a distance $$r$$ from a long wire carrying current $$i$$ is $$0.4\,T.$$ The magnetic field at a distance $$2r$$ is
A
$$0.2\,T$$
B
$$0.8\,T$$
C
$$0.1\,T$$
D
$$1.6\,T$$
Answer :
$$0.2\,T$$
106. A charged particle of charge $$q$$ and mass $$m$$ enters perpendicularly in a magnetic field $$B.$$ Kinetic energy of the particle is $$E,$$ then frequency of rotation is
A
$$\frac{{qB}}{{m\pi }}$$
B
$$\frac{{qB}}{{2\pi m}}$$
C
$$\frac{{qBE}}{{2\pi m}}$$
D
$$\frac{{qB}}{{2\pi E}}$$
Answer :
$$\frac{{qB}}{{2\pi m}}$$
107. An electron moving in a circular orbit of radius $$r$$ makes $$n$$ rotations per second. The magnetic field produced at the centre has magnitude
A
$$\frac{{{\mu _0}ne}}{{2\pi r}}$$
B
zero
C
$$\frac{{{\mu _0}{n^2}e}}{r}$$
D
$$\frac{{{\mu _0}ne}}{{2r}}$$
Answer :
$$\frac{{{\mu _0}ne}}{{2r}}$$
108. A steady current is flowing in a circular coil of radius $$R,$$ made up of a thin conducting wire. The magnetic field at the center of the loop is $${B_L}.$$ Now, a circular loop of radius $$\frac{R}{n}$$ is made form the same wire without changing its length, by unfolding and refolding the loop, and the same current is passed through it. If new magnetic field at the centre of the coil is $${B_C},$$ then the ratio $$\frac{{{B_L}}}{{{B_C}}}$$ is
A
$$1:{n^2}$$
B
$${n^{\frac{1}{2}}}$$
C
$$n:1$$
D
None of these
Answer :
$$1:{n^2}$$
109. A particle of charge $$ - 16 \times {10^{ - 18}}$$ coulomb moving with velocity $$10m{s^{ - 1}}$$ along the $$x$$-axis enters a region where a magnetic field of induction $$B$$ is along the $$y$$-axis, and an electric field of magnitude $${10^4}V/m$$ is along the negative $$z$$-axis. If the charged particle continues moving along the $$x$$-axis, the magnitude of $$B$$ is
A
$${10^3}Wb/{m^2}$$
B
$${10^5}Wb/{m^2}$$
C
$${10^{16}}Wb/{m^2}$$
D
$${10^{ - 3}}Wb/{m^2}$$
Answer :
$${10^3}Wb/{m^2}$$
110. Two long parallel wires are at a distance of $$1\,m.$$ Both of them carry $$1A$$ of current. The force of attraction per unit length between the two wires is
A
$$2 \times {10^{ - 7}}N/m$$
B
$$2 \times {10^{ - 8}}N/m$$
C
$$5 \times {10^{ - 8}}N/m$$
D
$${10^{ - 7}}N/m$$
Answer :
$$2 \times {10^{ - 7}}N/m$$