The charged particle will move along the lines of electric field (and magnetic field). Magnetic field will exert no force. The force by electric field will be along the lines of uniform electric field. Hence the particle will move in a straight line.

Using Ampere’s law at a distance $$r$$ from axis, $$B$$ is same from symmetry.
$$\int {B.dl = {\mu _0}i\,\,\,\,\,\,{\text{i}}{\text{.e}}{\text{.,}}\,B \times 2\pi r = {\mu _0}i} $$
Here $$i$$ is zero, for $$r < R,$$  whereas $$R$$ is the radius
$$\therefore B = 0$$

Let $$I$$ be current and $$l$$ be the length of the wire.
For I^st case:
$$B = \frac{{{\mu _0}In}}{{2r}} = \frac{{{\mu _0}I \times \pi }}{l}\,\,{\text{where}}\,2\pi r = l\,\,{\text{and}}\,\,n = 1$$
For II^nd case:
$$\eqalign{ & l = 2\left( {2\pi r'} \right) \Rightarrow r' = \frac{l}{{4\pi }} \cr & B' = \frac{{{\mu _0}nI}}{{2r'}} = \frac{{{\mu _0}2I}}{{2\frac{l}{{4\pi }}}} = \frac{{4{\mu _0}I\pi }}{l} = 4B \cr} $$

The wire carries a current $$I$$ in the negative $$z$$-direction. We have to consider the magnetic vector field
$$\overrightarrow B \,{\text{at}}\,\left( {x,y} \right)\,{\text{in}}\,{\text{the}}\,z = 0\,{\text{plane}}.$$
Magnetic field $$\overrightarrow B $$ is perpendicular to $$OP.$$
$$\eqalign{ & \therefore \overrightarrow B = B\sin \theta \hat i - B\cos \theta \hat j \cr & \sin \theta = \frac{y}{r},\,\cos \theta = \frac{x}{r},\,B = \frac{{{\mu _0}I}}{{2\pi r}} \cr & \therefore \overrightarrow B = \frac{{{\mu _0}I}}{{2\pi {r^2}}}\left( {y\hat i - x\hat j} \right) \cr & {\text{or,}}\,\overrightarrow B = \frac{{{\mu _0}I\left( {y\hat i - x\hat j} \right)}}{{2\pi \left( {{x^2} + {y^2}} \right)}} \cr} $$

Width of the magnetic field region $$\left( {b - a} \right) \leqslant R;$$   where $$'R'$$ is its radius of curvature inside magnetic field,
$$\therefore R = \frac{{mv}}{{qB}} \geqslant \left( {b - a} \right) \Rightarrow {v_{\min }} = \frac{{\left( {b - a} \right)qB}}{m}$$

The magnetic moment of a current carrying loop is given by $$\overrightarrow M = NI\overrightarrow A $$
Here $$N = 1,\,A = {a^2} + 2\pi {\left( {\frac{a}{2}} \right)^2} = {a^2}\left[ {1 + \frac{\pi }{2}} \right],$$         the direction is towards positive $$z$$-axis.
$$\therefore \overrightarrow M = I{a^2}\left[ {1 + \frac{\pi }{2}} \right]\hat k$$

Since, magnetic field is acting at right angles to the direction of motion of electron beams, so their paths will be circular.
$$\eqalign{ & r = \frac{{mv}}{{qB}} \cr & {\text{or}}\,\,r \propto v \cr & \therefore \frac{{{r_1}}}{{{r_2}}} = \frac{{{v_1}}}{{{v_2}}} = \frac{1}{2} \cr & {\text{or}}\,\,{r_1}:{r_2} = 1:2 \cr} $$

Here, $$\overrightarrow E $$ and $$\overrightarrow B $$ are perpendicular to each other and the velocity $$\overrightarrow v $$ does not change; therefore
$$qE = qvB \Rightarrow v = \frac{E}{B}$$
Also,
$$\left| {\frac{{\overrightarrow E \times \overrightarrow B }}{{{B^2}}}} \right| = \frac{{E\,B\sin \theta }}{{{B^2}}} = \frac{{E\,B\sin {{90}^ \circ }}}{{{B^2}}} = \frac{E}{B} = \left| {\overrightarrow v } \right| = v$$

$$\eqalign{ & {F_E} = qE\,\,\,\,\,\,\left( {{\text{Force due to electric field}}} \right) \cr & {F_B} = evB\sin \theta = qvB\sin \theta = 0\,\,\,\,\,\,\left( {{\text{Force due to magnetic field}}} \right) \cr} $$

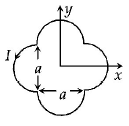
Force due to electric field will make the charged particle released from rest to move in the straight line (that of electric field). Since the force due to magnetic field is zero, therefore, the charged particle will move in a straight line.

$$\eqalign{ & {i_g} = i\left( {\frac{{SG}}{{S + G}}} \right) \cr & {\text{or}}\,\,50 \times {10^{ - 6}} = i\left( {\frac{S}{{S + 100}}} \right)\,......\left( {\text{i}} \right) \cr & {\text{Also}}\,\,V = {i_g}\left( {G + {R_0}} \right) \cr & {\text{or}}\,\,V = 50 \times {10^{ - 6}}\left( {100 + {R_0}} \right)\,......\left( {{\text{ii}}} \right) \cr} $$
On simplifying above equations, we get
$$V = 10\,V,{R_0} = 200 \times {10^{ - 3}}\,\Omega $$