111. The time period of a charged particle undergoing a circular motion in a uniform magnetic field is independent of its
A
speed
B
mass
C
charge
D
magnetic induction
Answer :
speed
112.
The magnetic field at, point $$'C'$$ due to current flowing in $$'M'$$ shape figure is

A
$$\frac{{{\mu _0}}}{{2\pi }}.\frac{{\sqrt 3 i}}{\ell }$$
B
$$\frac{{{\mu _0}}}{\pi }.\frac{i}{\ell }\sqrt 3 $$
C
zero
D
$$\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{{\ell \sqrt 3 }}$$
Answer :
$$\frac{{{\mu _0}}}{\pi }.\frac{i}{\ell }\sqrt 3 $$
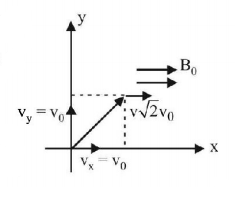
113. A charged particle of specific charge $$\left( {\frac{{{\text{charge}}}}{{{\text{mass}}}}} \right)\alpha $$ is released from origin at time $$t = 0$$ with velocity $$\vec v = {v_0}\left( {\hat i + \hat j} \right)$$ in uniform magnetic field $$\vec B = {B_0}\hat i.$$ Coordinates of the particle at time $$t = \frac{\pi }{{\left( {{B_0}\alpha } \right)}}$$ are
A
$$\left( {\frac{{{v_0}}}{{2{B_0}\alpha }},\frac{{\sqrt 2 {v_0}}}{{\alpha {B_0}}},\frac{{ - {v_0}}}{{{B_0}\alpha }}} \right)$$
B
$$\left( {\frac{{ - {v_0}}}{{2{B_0}\alpha }},0,0} \right)$$
C
$$\left( {0,\frac{{2{v_0}}}{{{B_0}\alpha }},\frac{{{v_0}\pi }}{{2{B_0}\alpha }}} \right)$$
D
$$\left( {\frac{{{v_0}\pi }}{{{B_0}\alpha }},0,\frac{{ - 2{v_0}}}{{{B_0}\alpha }}} \right)$$
Answer :
$$\left( {\frac{{{v_0}\pi }}{{{B_0}\alpha }},0,\frac{{ - 2{v_0}}}{{{B_0}\alpha }}} \right)$$
114. Two identical long conducting wires $$AOB$$ and $$COD$$ are placed at right angle to each other, with one above other such that $$'O'$$ is their common point for the two. The wires carry $${I_1}$$ and $${I_2}$$ currents respectively. Point $$'P'$$ is lying at distance $$'d'$$ from $$'O'$$ along a direction perpendicular to the plane containing the wires. The magnetic field at the point $$'P'$$ will be:
A
$$\frac{{{\mu _0}}}{{2\pi d}}\left( {\frac{{{I_1}}}{{{I_2}}}} \right)$$
B
$$\frac{{{\mu _0}}}{{2\pi d}}\left( {{I_1} + {I_2}} \right)$$
C
$$\frac{{{\mu _0}}}{{2\pi d}}\left( {I_1^2 - I_2^2} \right)$$
D
$$\frac{{{\mu _0}}}{{2\pi d}}{\left( {I_1^2 + I_2^2} \right)^{\frac{1}{2}}}$$
Answer :
$$\frac{{{\mu _0}}}{{2\pi d}}{\left( {I_1^2 + I_2^2} \right)^{\frac{1}{2}}}$$
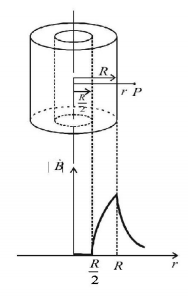
115. An infinitely long hollow conducting cylinder with inner radius $$\frac{R}{2}$$ and outer radius $$R$$ carries a uniform current density along its length. The magnitude of the magnetic field, $$\left| {\vec B} \right|$$ as a function of the radial distance $$r$$ from the axis is best represented by
A


B


C


D


Answer :


116.
A wire carrying current $$I$$ has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to $$X$$-axis while semicircular portion of radius $$R$$ is lying in $$Y-Z$$ plane. Magnetic field at point $$O$$ is

A
$$B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
B
$$B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i - 2\hat k} \right)$$
C
$$B = - \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
D
$$B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i - 2\hat k} \right)$$
Answer :
$$B = \frac{{{\mu _0}}}{{4\pi }}\frac{I}{R}\left( {\pi \hat i + 2\hat k} \right)$$
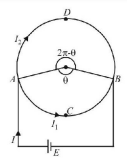
117. A battery is connected between two points $$A$$ and $$B$$ on the circumference of a uniform conducting ring of radius $$r$$ and resistance $$R.$$ One of the arcs $$AB$$ of the ring subtends an angle $$\theta $$ at the centre. The value of the magnetic induction at the centre due to the current in the ring is
A
proportional to $$2\left( {{{180}^ \circ } - \theta } \right)$$
B
inversely proportional to $$r$$
C
zero, only if $$\theta = {180^ \circ }$$
D
zero for all values of $$\theta $$
Answer :
zero for all values of $$\theta $$
118. Five very long, straight insulated wires are closely bound together to form a small cable. Currents carried by the wires are : $${I_1} = 20\,A,{I_2} = - 6\,A,{I_3} = 12\,A,{I_4} = - 7\,A,{I_5} = 18\,A.$$ (Negative currents are opposite in direction to the positive). The magnetic field induction at a distance of $$10\,cm$$ from the cable is
A
$$5\,\mu T$$
B
$$15\,\mu T$$
C
$$74\,\mu T$$
D
$$128\,\mu T$$
Answer :
$$74\,\mu T$$
119. A beam of electrons is moving with constant velocity in a region having simultaneous perpendicular electric and magnetic fields of strength $$20\,V{m^{ - 1}}$$ and $$0.5\,T,$$ respectively at right angles to the direction of motion of the electrons. Then, the velocity of electrons must be
A
$$8\,m/s$$
B
$$20\,m/s$$
C
$$40\,m/s$$
D
$$\frac{1}{{40}}m/s$$
Answer :
$$40\,m/s$$
120. A cyclotron is operated at an oscillator frequency of $$24\,MHz$$ and has a dee radius $$R = 60\,cm.$$ What is magnitude of the magnetic field $$B$$ (in Tesla) to accelerate deuterons $$\left( {{\text{mass}} = 3.34 \times {{10}^{ - 27}}} \right)kg$$ ?
A
9.5
B
7.2
C
5.0
D
3.2
Answer :
3.2