141. When a proton is released from rest in a room, it starts with an initial acceleration $${a_0}$$ towards West. When it is projected towards North with a speed $${v_0}$$ it moves with an initial acceleration $${3a_0}$$ towards West. The electric and magnetic fields in the room are
A
$$\frac{{m{a_0}}}{e}\,{\text{West,}}\,\frac{{2m{a_0}}}{{e{v_0}}}\,{\text{up}}$$
B
$$\frac{{m{a_0}}}{e}\,{\text{West,}}\,\frac{{2m{a_0}}}{{e{v_0}}}\,{\text{down}}$$
C
$$\frac{{m{a_0}}}{e}\,{\text{East,}}\,\frac{{3m{a_0}}}{{e{v_0}}}\,{\text{up}}$$
D
$$\frac{{m{a_0}}}{e}\,{\text{East,}}\,\frac{{3m{a_0}}}{{e{v_0}}}\,{\text{down}}$$
Answer :
$$\frac{{m{a_0}}}{e}\,{\text{West,}}\,\frac{{2m{a_0}}}{{e{v_0}}}\,{\text{down}}$$
142. The magnetic moment of a circular coil carrying current is
A
directly proportional to the length of the wire in the coil
B
inversely proportional to the length of the wire in the coil
C
directly proportional to the square of the length of the wire in the coil
D
inversely proportional to the square of the length of the wire in the coil
Answer :
directly proportional to the square of the length of the wire in the coil
143.
Two identical particles having the same mass $$m$$ and charges $$+q$$ and $$-q$$ separated by a distance $$d$$ enter a uniform magnetic field $$B$$ directed perpendicular to paper inwards with in speeds $${v_1}$$ and $${v_2}$$ as shown in Fig. The particles will not collide if
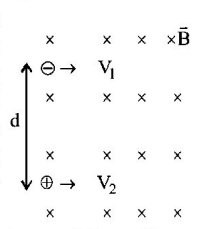
A
$$d > \frac{m}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
B
$$d < \frac{m}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
C
$$d > \frac{{2m}}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
D
$${v_1} = {v_2}$$
Answer :
$$d > \frac{{2m}}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
144. In an ammeter $$0.2\% $$ of main current passes through the galvanometer. If resistance of galvanometer is $$G,$$ the resistance of ammeter will be:
A
$$\frac{1}{{499}}G$$
B
$$\frac{{499}}{{500}}G$$
C
$$\frac{1}{{500}}G$$
D
$$\frac{{500}}{{499}}G$$
Answer :
$$\frac{1}{{500}}G$$
145. A current $$I$$ flows in an infinitely long wire with cross section in the form of a semi-circular ring of radius $$R.$$ The magnitude of the magnetic induction along its axis is:
A
$$\frac{{{\mu _0}I}}{{2{\pi ^2}R}}$$
B
$$\frac{{{\mu _0}I}}{{2\pi R}}$$
C
$$\frac{{{\mu _0}I}}{{4\pi R}}$$
D
$$\frac{{{\mu _0}I}}{{{\pi ^2}R}}$$
Answer :
$$\frac{{{\mu _0}I}}{{{\pi ^2}R}}$$
146. Three particles, an electron $$\left( e \right),$$ a proton $$\left( p \right)$$ and a helium atom $$\left( He \right)$$ are moving in circular paths with constant speeds in the $$x - y$$ plane in a region where a uniform magnetic field $$B$$ exists along $$z$$-axis. The times taken by $$e,p$$ and $$He$$ inside the field to complete one revolution are $${t_e},{t_p}$$ and $${t_{He}}$$ respectively. Then,
A
$${t_{He}} > {t_p} = {t_e}$$
B
$${t_{He}} > {t_p} > {t_e}$$
C
$${t_{He}} = {t_p} = {t_e}$$
D
None of these
Answer :
$${t_{He}} > {t_p} > {t_e}$$
147.
An infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The redius of the loop is $$a$$ and distance of its centre from the wire is $$d\left( {d > > a} \right).$$ If the loop applies a force $$F$$ on the wire then:

A
$$F = 0$$
B
$$F \propto \left( {\frac{a}{d}} \right)$$
C
$$F \propto \left( {\frac{{{a^2}}}{{{d^3}}}} \right)$$
D
$$F \propto {\left( {\frac{a}{d}} \right)^2}$$
Answer :
$$F \propto {\left( {\frac{a}{d}} \right)^2}$$
148.
A uniform magnetic field is directed out of the page. A charged particle, moving in the plane of the page, follows a clockwise spiral of decreasing radius as shown. A reasonable explanation is
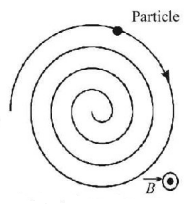
A
the charge is positive and slowing down
B
the charge is negative and slowing down
C
the charge is positive and speeding up
D
the charge is negative and speeding up
Answer :
the charge is positive and slowing down
149. Two concentric coils each of radius equal to 2 $$\pi \,cm$$ are placed at right angles to each other. 3 ampere and 4 ampere are the currents flowing in each coil respectively. The magnetic induction in $$Weber/{m^2}$$ at the centre of the coils will be $$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}Wb/A.m} \right)$$
A
$${10^{ - 5}}$$
B
$$12 \times {10^{ - 5}}$$
C
$$7 \times {10^{ - 5}}$$
D
$$5 \times {10^{ - 5}}$$
Answer :
$$5 \times {10^{ - 5}}$$
150.
An on-planar loop of conducting wire carrying a current $$I$$ is placed as shown in the figure. Each of the straight sections of the loop is of length $$2a.$$ The magnetic field due to this loop at the point $$P\left( {a,0,a} \right)$$ points in the direction

A
$$\frac{1}{{\sqrt 2 }}\left( { - \hat j + \hat k} \right)$$
B
$$\frac{1}{{\sqrt 3 }}\left( { - \hat j + \hat k + \hat i} \right)$$
C
$$\frac{1}{{\sqrt 3 }}\left( {\hat i + \hat j + \hat k} \right)$$
D
$$\frac{1}{{\sqrt 2 }}\left( {\hat i + \hat k} \right)$$
Answer :
$$\frac{1}{{\sqrt 2 }}\left( {\hat i + \hat k} \right)$$





