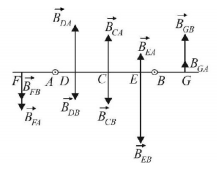
171. Two long parallel wires are at a distance $$2d$$ apart. They carry steady equal currents flowing out of the plane of the paper, as shown. The variation of the magnetic field $$B$$ along the line $$XX’$$ is given by
A
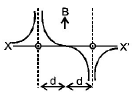

B
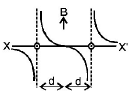

C


D
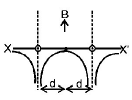

Answer :


172. Two similar coils of radius $$R$$ are lying concentrically with their planes at right angles to each other. The currents flowing in them are $$I$$ and $$2I,$$ respectively. The resultant magnetic field induction at the centre will be
A
$$\frac{{\sqrt 5 {\mu _0}I}}{{2R}}$$
B
$$\frac{{3{\mu _0}I}}{{2R}}$$
C
$$\frac{{{\mu _0}I}}{{2R}}$$
D
$$\frac{{{\mu _0}I}}{R}$$
Answer :
$$\frac{{\sqrt 5 {\mu _0}I}}{{2R}}$$
173. A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
A
the velocity
B
the momentum
C
the kinetic energy
D
None of these
Answer :
the kinetic energy
174. An alternating electric field of frequency $$\nu ,$$ is applied across the dees (radius = $$R$$ ) of a cyclotron that is being used to accelerate protons (mass = $$m$$). The operating magnetic field $$\left( B \right)$$ used in the cyclotron and the kinetic energy $$\left( K \right)$$ of the proton beam, produced by it, are given by
A
$$B = \frac{{m\nu }}{e}\,{\text{and}}\,\,K = 2m{\pi ^2}{\nu ^2}{R^2}$$
B
$$B = \frac{{2\pi m\nu }}{e}\,{\text{and}}\,\,K = {m^2}\pi \nu {R^2}$$
C
$$B = \frac{{2\pi m\nu }}{e}\,{\text{and}}\,\,K = 2m{\pi ^2}{\nu ^2}{R^2}$$
D
$$B = \frac{{m\nu }}{e}\,{\text{and}}\,\,K = {m^2}\pi \nu {R^2}$$
Answer :
$$B = \frac{{2\pi m\nu }}{e}\,{\text{and}}\,\,K = 2m{\pi ^2}{\nu ^2}{R^2}$$
175. An alternating electric field, of frequency $$v,$$ is applied across the dees (radius = $$R$$ ) of a cyclotron that is being used to accelerate protons (mass = $$m$$). The operating magnetic field $$\left( B \right)$$ used in the cyclotron and the kinetic energy $$\left( K \right)$$ of the proton beam, produced by it, are given by :
A
$$B = \frac{{m\upsilon }}{e}\,{\text{and}}\,K = 2m{\pi ^2}{\upsilon ^2}{R^2}$$
B
$$B = \frac{{2\pi m\upsilon }}{e}\,{\text{and}}\,K = {m^2}\pi \upsilon {R^2}$$
C
$$B = \frac{{2\pi m\upsilon }}{e}\,{\text{and}}\,K = 2m{\pi ^2}{\upsilon ^2}{R^2}$$
D
$$B = \frac{{m\upsilon }}{e}\,{\text{and}}\,K = {m^2}\pi \upsilon {R^2}$$
Answer :
$$B = \frac{{2\pi m\upsilon }}{e}\,{\text{and}}\,K = 2m{\pi ^2}{\upsilon ^2}{R^2}$$
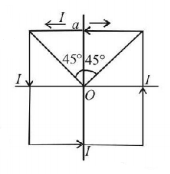
176. A current $$I$$ flows in the anticlockwise direction through a square loop of side a lying in the $$XOY$$ plane with its center at the origin. The magnetic induction at the center of the square loop is
A
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}{{\hat e}_x}$$
B
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}{{\hat e}_z}$$
C
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi {a^2}}}{{\hat e}_z}$$
D
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi {a^2}}}{{\hat e}_x}$$
Answer :
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}{{\hat e}_z}$$
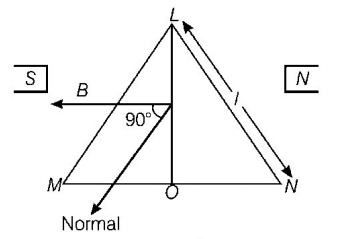
177. A coil in the shape of an equilateral triangle of side $$l$$ is suspended between the pole pieces of a permanent magnet such that $$B$$ is in plane of the coil. If due to a current $$i$$ in the triangle a torque $$\tau $$ acts on it, the side $$l$$ of the triangle is
A
$$\frac{2}{{\sqrt 3 }}{\left( {\frac{\tau }{{Bi}}} \right)^{\frac{1}{2}}}$$
B
$$\frac{2}{{\sqrt 3 }}\left( {\frac{\tau }{{Bi}}} \right)$$
C
$$2{\left( {\frac{\tau }{{\sqrt 3 Bi}}} \right)^{\frac{1}{2}}}$$
D
$$\frac{1}{{\sqrt 3 }}\frac{\tau }{{Bi}}$$
Answer :
$$2{\left( {\frac{\tau }{{\sqrt 3 Bi}}} \right)^{\frac{1}{2}}}$$
178. The magnetic field lines due to a bar magnet are correctly shown in
A


B
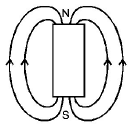

C
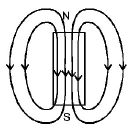

D


Answer :


179. A thin rectangular magnet suspended freely has a period of oscillation equal to $$T.$$ Now it is broken into two equal halves (each having half of the original length) and one piece is made to oscillate freely in the same field. If its period of oscillation is $$T’,$$ the ratio $$\frac{{T'}}{T}$$ is
A
$$\frac{1}{{2\sqrt 2 }}$$
B
$$\frac{1}{2}$$
C
2
D
$$\frac{1}{4}$$
Answer :
$$\frac{1}{2}$$
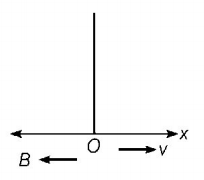
180. A charge moving with velocity $$v$$ in $$x$$-direction is subjected to a field of magnetic induction in negative $$x$$-direction. As a result, the charge will
A
remain unaffected
B
start moving in a circular $$y$$ - $$z$$ plane
C
retard along $$x$$-axis
D
move along a helical path around $$x$$-axis
Answer :
remain unaffected