181. If in a circular coil $$A$$ of radius $$R,$$ current $$I$$ is flowing and in another coil $$B$$ of radius $$2R$$ a current $$2I$$ is flowing, then the ratio of the magnetic fields $${B_A}$$ and $${B_B},$$ produced by them will be
A
$$1$$
B
$$2$$
C
$$\frac{1}{2}$$
D
$$4$$
Answer :
$$1$$
182. Two long conductors, separated by a distance $$d$$ carry current $${I_1}$$ and $${I_2}$$ in the same direction. They exert a force $$F$$ on each other. Now the current in one of them is increased to two times and its direction is reversed. The distance is also increased to $$3d.$$ The new value of the force between them is
A
$$ - \frac{{2F}}{3}$$
B
$$\frac{F}{3}$$
C
$$ - 2F$$
D
$$ - \frac{F}{3}$$
Answer :
$$ - \frac{{2F}}{3}$$
183. An electron enters a region where magnetic field $$\left( B \right)$$ and electric field $$\left( E \right)$$ are mutually perpendicular, then
A
it will always move in the direction of $$B$$
B
it will always move in the direction of $$E$$
C
it always possess circular motion
D
it can go undeflected also
Answer :
it can go undeflected also
184. The magnetic induction at a point $$P$$ which is at the distance of $$4\,cm$$ from a long current carrying wire is $${10^{ - 3}}T.$$ The field of induction at a distance $$12\,cm$$ from the current will be
A
$$3.33 \times {10^{ - 4}}T$$
B
$$1.11 \times {10^{ - 4}}T$$
C
$$3 \times {10^{ - 3}}T$$
D
$$9 \times {10^{ - 3}}T$$
Answer :
$$3.33 \times {10^{ - 4}}T$$
185. A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
A
its velocity will increase
B
Its velocity will decrease
C
it will turn towards left of direction of motion
D
it will turn towards right of direction of motion
Answer :
Its velocity will decrease
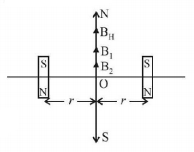
186. Two short bar magnets of length $$1 cm$$ each have magnetic moments $$1.20\,A{m^2}$$ and $$1.00\,A{m^2}$$ respectively. They are placed on a horizontal table parallel to each other with their $$N$$ poles pointing towards the South. They have a common magnetic equator and are separated by a distance of $$20.0 cm.$$ The value of the resultand horizontal magnetic induction at the mid-point $$O$$ of the line joining their centres is close to (Horizontal component of earth.s magnetic induction is $$3.6 \times 10.5\,Wb/{m^2}$$ )
A
$$3.6 \times 10.5\,Wb/{m^2}$$
B
$$2.56 \times 10.4\,Wb/{m^2}$$
C
$$3.50 \times 10.4\,Wb/{m^2}$$
D
$$5.80 \times 10.4\,Wb/{m^2}$$
Answer :
$$2.56 \times 10.4\,Wb/{m^2}$$
187. A particle of mass $$M$$ and charge $$Q$$ moving with velocity $$\vec v$$ describe a circular path of radius $$R$$ when subjected to a uniform transverse magnetic field of induction $$B.$$ The work done by the field when the particle completes one full circle is
A
$$\left( {\frac{{M{v^2}}}{R}} \right)2\pi R$$
B
zero
C
$$BQ2\pi R$$
D
$$BQv2\pi R$$
Answer :
zero
188. An ionized gas contains both positive and negative ions. If it is subjected simultaneously to an electric field along the $$+x$$ -direction and a magnetic field along the $$+z$$ -direction, then
A
positive ions deflect towards $$+y$$ -direction and negative ions towards $$-y$$ -direction
B
all ions deflect towards $$+y$$ -direction
C
all ions deflect towards $$-y$$ -direction
D
positive ions deflect towards $$-y$$ -direction and negative ions towards $$+y$$ -direction.
Answer :
all ions deflect towards $$-y$$ -direction
189.
A circular arc $$QTS$$ is kept in an external magnetic field $${{\vec B}_0}$$ as shown in figure. The arc carries a current $$I.$$ The magnetic field is directed normal and into the page. The force acting on the arc is
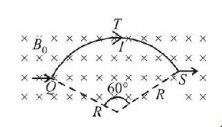
A
$$2I{B_0}R\hat k$$
B
$$I{B_0}R\hat k$$
C
$$ - 2I{B_0}R\hat k$$
D
$$ - I{B_0}R\hat k$$
Answer :
$$I{B_0}R\hat k$$
190. A charge $$q$$ moves in a region where electric field $$E$$ and magnetic field $$B$$ both exist, then the force on it is
A
$$q\left( {v \times B} \right)$$
B
$$qE + q\left( {v \times B} \right)$$
C
$$qB + q\left( {B \times v} \right)$$
D
$$qB + q\left( {E \times v} \right)$$
Answer :
$$qE + q\left( {v \times B} \right)$$