161. Current is flowing in a coil of area $$A$$ and number of turns $$N,$$ then magnetic moment of the coil, $$M$$ is equal to
A
$$NiA$$
B
$$\frac{{Ni}}{A}$$
C
$$\frac{{Ni}}{{\sqrt A }}$$
D
$${N^2}Ai$$
Answer :
$$NiA$$
162.
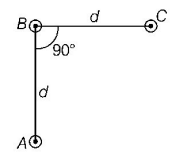
An arrangement of three parallel straight wires placed perpendicular to plane of paper carrying same current $$I$$ along the same direction is shown in figure. Magnitude of force per unit length on the middle wire $$B$$ is given by
A
$$\frac{{{\mu _0}{i^2}}}{{2\pi d}}$$
B
$$\frac{{2{\mu _0}{i^2}}}{{\pi d}}$$
C
$$\frac{{\sqrt 2 {\mu _0}{i^2}}}{{\pi d}}$$
D
$$\frac{{{\mu _0}{i^2}}}{{\sqrt 2 \pi d}}$$
Answer :
$$\frac{{{\mu _0}{i^2}}}{{\sqrt 2 \pi d}}$$
163. The magnetic lines of force inside a bar magnet
A
are from north-pole to south-pole of the magnet
B
do not exist
C
depend upon the area of cross-section of the bar magnet
D
are from south-pole to north-pole of the Magnet
Answer :
are from south-pole to north-pole of the Magnet
164. When a current of $$5 mA$$ is passed through a galvanometer having a coil of resistance $$15\,\Omega $$ it shows full scale deflection. The value of the resistance to be put in series with the galvanometer to convert it into to voltmeter of range $$0 - 10 V$$ is
A
$$2.535 \times {10^3}\Omega $$
B
$$4.005 \times {10^3}\Omega $$
C
$$1.985 \times {10^3}\Omega $$
D
$$2.045 \times {10^3}\Omega $$
Answer :
$$1.985 \times {10^3}\Omega $$
165. Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field $${B_1},$$ at its centre when a current $$I$$ passes through it. The ratio $${B_1}:{B_2}$$ is:
A
$$1:1$$
B
$$1:3$$
C
$$1:9$$
D
$$9:1$$
Answer :
$$1:3$$
166.
A conducting wire bent in the form of a parabola $${y^2} = 2x$$ carries a current $$i = 2\,A$$ as shown in figure. This wire is placed in a uniform magnetic field $$\overrightarrow B = - 4\hat k\,tesla.$$ The magnetic force on the wire (in newton)

A
$$ - 16\hat i$$
B
$$ 32\hat i$$
C
$$ - 32\hat i$$
D
$$16\hat i$$
Answer :
$$ 32\hat i$$
167. At what distance from a long straight wire carrying a current of $$12\,A$$ will the magnetic field be equal to $$3 \times {10^{ - 5}}Wb/{m^2}$$ ?
A
$$8 \times {10^{ - 2}}m$$
B
$$12 \times {10^{ - 2}}m$$
C
$$18 \times {10^{ - 2}}m$$
D
$$24 \times {10^{ - 2}}m$$
Answer :
$$8 \times {10^{ - 2}}m$$
168. A horizontal overhead powerline is at height of $$4m$$ from the ground and carries a current of $$100A$$ from east to west. The magnetic field directly below it on the ground is $$\left( {{\mu _0} = 4\pi \times {{10}^{ - 7}}Tm\,{A^{ - 1}}} \right)$$
A
$$2.5 \times {10^{ - 7}}T\,{\text{southward}}$$
B
$$5 \times {10^{ - 6}}T\,{\text{northward}}$$
C
$$5 \times {10^{ - 6}}T\,{\text{southward}}$$
D
$$2.5 \times {10^{ - 7}}T\,{\text{northward}}$$
Answer :
$$5 \times {10^{ - 6}}T\,{\text{southward}}$$
169. A beam of electrons passes undeflected through mutually perpendicular electric and magnetic fields. If the electric field is switched OFF and the same magnetic field is maintained, the electrons move
A
in an elliptical orbit
B
in a circular orbit
C
along a parabolic path
D
along a straight line
Answer :
in a circular orbit
170. The magnetic field due to a current carrying circular loop of radius $$3\,cm$$ at a point on the axis at a distance of $$4\,cm$$ from the centre is $$54\,\mu T.$$ What will be its value at the centre of loop ?
A
$$125\,\mu T$$
B
$$150\,\mu T$$
C
$$250\,\mu T$$
D
$$75\,\mu T$$
Answer :
$$250\,\mu T$$