151. A charged particle of mass $$m$$ and charge $$q$$ travels on a circular path of radius $$r$$ that is perpendicular to a magnetic field $$B.$$ The time taken by the particle to complete one revolution is
A
$$\frac{{2\pi {q^2}B}}{m}$$
B
$$\frac{{2\pi mq}}{B}$$
C
$$\frac{{2\pi m}}{{qB}}$$
D
$$\frac{{2\pi qB}}{m}$$
Answer :
$$\frac{{2\pi m}}{{qB}}$$
152. A moving coil galvanometer has resistance $$50\,\Omega $$ and it indicates full deflection at $$4 mA$$ current. A voltmeter is made using this galvanometer and a $$5k\Omega $$ resistance. The maximum voltage, that can be measured using this voltmeter, will be close to:
A
$$40 V$$
B
$$15 V$$
C
$$20 V$$
D
$$10 V$$
Answer :
$$20 V$$
153. If a long hollow copper pipe carries a current, then magnetic field is produced
A
inside the pipe only
B
outside the pipe only
C
both inside and outside the pipe
D
no where
Answer :
outside the pipe only
154.
A magnetic field $$\overrightarrow B = {B_0}\hat j,$$ exists in the region $$a < x < 2a,$$ and $$\overrightarrow B = - {B_0}\hat j,$$ in the region $$2a < x < 3a,$$ where $${B_0}$$ is a positive constant. A positive point charge moving with a velocity $$v = {v_0}\hat i,$$ where $${v_0}$$ is a positive constant, enters the magnetic field at $$x = a.$$ The trajectory of the charge in this region can be like
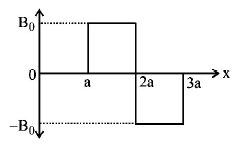
A
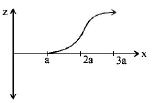

B
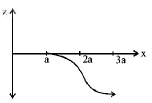

C


D
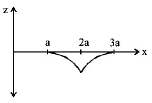

Answer :


155. An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii $${r_e},{r_p},{r_\alpha }$$ respectively in a uniform magnetic field $$B.$$ The relation between $${r_e},{r_p},{r_\alpha }$$ is:
A
$${r_e} > {r_p} = {r_\alpha }$$
B
$${r_e} < {r_p} = {r_\alpha }$$
C
$${r_e} < {r_p} < {r_\alpha }$$
D
$${r_e} < {r_\alpha } < {r_p}$$
Answer :
$${r_e} < {r_p} = {r_\alpha }$$
156. A charged particle enters in a magnetic field in a direction perpendicular to the magnetic field. Which of the following graphs show the correct variation of kinetic energy of the particle with time $$t$$ ?
A
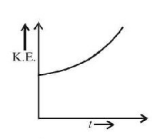

B
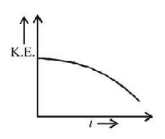

C
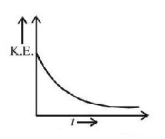

D
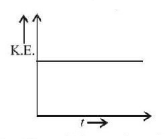

Answer :


157. An electron moves in a circular orbit with a uniform speed $$v.$$ It produces a magnetic field $$B$$ at the centre of the circle. The radius of the circle is proportional to
A
$$\frac{B}{v}$$
B
$$\frac{v}{B}$$
C
$$\sqrt {\frac{v}{B}} $$
D
$$\sqrt {\frac{B}{v}} $$
Answer :
$$\sqrt {\frac{v}{B}} $$
158. A helium nucleus makes a full rotation in a circle of radius $$0.8$$ meter in $$2\,\sec.$$ The value of the magnetic field induction $$B$$ in tesla at the centre of circle will be
A
$$2 \times {10^{ - 19}}{\mu _0}$$
B
$$\frac{{{{10}^{ - 19}}}}{{{\mu _0}}}$$
C
$${10^{ - 19}}{\mu _0}$$
D
$$\frac{{2 \times {{10}^{ - 20}}}}{{{\mu _0}}}$$
Answer :
$${10^{ - 19}}{\mu _0}$$
159.
A charged particle moves insides a pipe which is bent as shown in fig. If $$R > \frac{{mv}}{{qB}},$$ then force exerted by the pipe on charged particle at $$P$$ is (Neglect gravity)

A
toward center
B
away from center
C
zero
D
none of these
Answer :
toward center
160. The dipole moment of a circular loop carrying a current $$I,$$ is $$m$$ and the magnetic field at the centre of the loop is $${B_1}.$$ When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is $${B_2}.$$ The ratio $$\frac{{{B_1}}}{{{B_2}}}$$ is:
A
$$2$$
B
$$\sqrt 3 $$
C
$$\sqrt 2 $$
D
$$\frac{1}{{\sqrt 2 }}$$
Answer :
$$\sqrt 2 $$