21. Fuse wire is a wire of
A
low resistance and low melting point
B
low resistance and high melting point
C
high resistance and high melting point
D
high resistance and low melting point
Answer :
high resistance and low melting point
22. A potentiometer wire is $$100\,cm$$ long and a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obtained at $$50\,cm$$ and $$10\,cm$$ from the positive end of the wire in the two cases. The ratio of emf is
A
$$5:4$$
B
$$3:4$$
C
$$3:2$$
D
$$5:1$$
Answer :
$$3:2$$
23. The resistance of a wire is $$R.$$ It is bent at the middle by $${180^ \circ }$$ and both the ends are twisted together to make a shorter wire. The resistance of the new wire is
A
$$2R$$
B
$$\frac{R}{2}$$
C
$$\frac{R}{4}$$
D
$$\frac{R}{8}$$
Answer :
$$\frac{R}{4}$$
24.
In the circuit shown in the figure, if potential at point $$A$$ is taken to be zero, the potential at point $$B$$ is

A
$$ - 1\,V$$
B
$$ + 2V$$
C
$$ - 2V$$
D
$$ + 1\,V$$
Answer :
$$ + 1\,V$$
25. Three equal resistors connected in series across a source of emf together dissipate $$10\,W$$ of power. What will be the power dissipated in watt if the same resistors are connected in parallel across the same source of emf ?
A
$$\frac{{10}}{3}$$
B
$$10$$
C
$$30$$
D
$$90$$
Answer :
$$90$$
26. The electrochemical equivalent of a metal is $${3.35109^{ - 7}}kg$$ per Coulomb. The mass of the metal liberated at the cathode when a $$3A$$ current is passed for 2 seconds will be
A
$$6.6 \times {10^{57}}kg$$
B
$$9.9 \times {10^{ - 7}}kg$$
C
$$19.8 \times {10^{ - 7}}kg$$
D
$$1.1 \times {10^{ - 7}}kg$$
Answer :
$$19.8 \times {10^{ - 7}}kg$$
27.
In the circuit shown in the figure, find the current in $$45\,\Omega .$$

A
$$4\,A$$
B
$$2.5\,A$$
C
$$2\,A$$
D
None of these
Answer :
$$2\,A$$
28.
A resistance is shown in the figure. Its value and tolerance are given respectively by:

A
$$270\,\Omega ,\,10\% $$
B
$$27k\,\Omega ,\,10\% $$
C
$$27k\,\Omega ,\,20\% $$
D
$$270\,\Omega ,\,5\% $$
Answer :
$$27k\,\Omega ,\,10\% $$
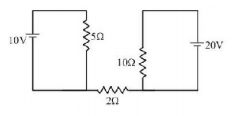
29.
Find out the value of current through $$2\,\Omega $$ resistance for the given circuit.

A
zero
B
$$2A$$
C
$$5A$$
D
$$4A$$
Answer :
zero
30.
Six identical resistors are connected as shown in the figure. The equivalent resistance will be
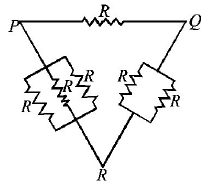
A
Maximum between $$P$$ and $$R$$
B
Maximum between $$Q$$ and $$R$$
C
Maximum between $$P$$ and $$Q$$
D
All are equal
Answer :
Maximum between $$P$$ and $$Q$$