51.
A potentiometer arrangement is shown in fig. The driver cell has emf $$e$$ and internal resistance $$r.$$ The resistance of potentiometer wire $$AB$$ is $$R.$$ $$F$$ is the cell of $$em\,\frac{e}{3}$$ and internal resistance $$\frac{r}{3}.$$ Balance point $$\left( J \right)$$ can be obtained for all finite values of

A
$$R > \frac{r}{2}$$
B
$$R < \frac{r}{2}$$
C
$$R > \frac{r}{3}$$
D
$$R < \frac{r}{3}$$
Answer :
$$R > \frac{r}{2}$$
52. A copper wire is stretched to make it $$0.5\% $$ longer. The percentage change in its electrical resistance if its volume remains unchanged is:
A
$$2.0\% $$
B
$$2.5\% $$
C
$$1.0\% $$
D
$$0.5\% $$
Answer :
$$1.0\% $$
53.
What will be the change in the resistance of a circuit consisting of five identical conductors if two similar conductors are added as shown by the dashed line in figure.

A
becomes $$\frac{1}{5}$$ times
B
becomes $$\frac{3}{5}$$ times
C
becomes $$\frac{2}{5}$$ times
D
becomes $$\frac{1}{2}$$ times
Answer :
becomes $$\frac{3}{5}$$ times
54.
In the circuit shown, current (in $$A$$) through $$50\,V$$ and $$30\,V$$ batteries are, respectively.

A
2.5 and 3
B
3.5 and 2
C
4.5 and 1
D
3 and 2.5
Answer :
2.5 and 3
55. A wire of radius $$r$$ and another wire of radius $$2r,$$ both of same material and length are connected in series to each other. The combination is connected across a battery. The ratio of the heats produced in the two wires will be
A
4.00
B
2.00
C
0.50
D
0.25
Answer :
4.00
56.
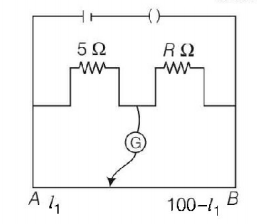
The resistances in the two arms of the meter bridge are $$5\,\Omega $$ and $$R\,\Omega ,$$ respectively. When the resistance $$R$$ is shunted with an equal resistance, the new balance point is at $$1.6\,{l_1}.$$ The resistance $$R,$$ is
A
$$10\,\Omega $$
B
$$15\,\Omega $$
C
$$20\,\Omega $$
D
$$25\,\Omega $$
Answer :
$$15\,\Omega $$
57.
A wire of resistance $$12\,\Omega {m^{ - 1}}$$ is bent to form a complete circle of radius $$10\,cm.$$ The resistance between its two diametrically opposite points $$A$$ and $$B$$ as shown in the figure is

A
$$0.6\,\pi \,\Omega $$
B
$$3\,\Omega $$
C
$$6\,\pi \,\Omega $$
D
$$6\,\Omega $$
Answer :
$$0.6\,\pi \,\Omega $$
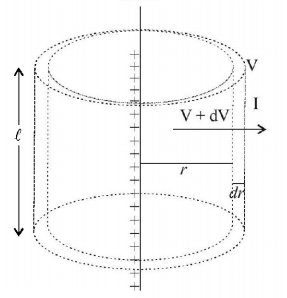
58. An infinite line charge of uniform electric charge density $$\lambda $$ lies along the axis of an electrically conducting infinite cylindrical shell of radius $$R.$$ At time $$t = 0,$$ the space inside the cylinder is filled with a material of permittivity $$\varepsilon $$ and electrical conductivity $$\sigma .$$ The electrical conduction in the material follows Ohm's law. Which one of the following graphs best describes the subsequent variation of the magnitude of current density $$j\left( t \right)$$ at any point in the material?
A


B


C


D


Answer :


59. A spherical black body with a radius of $$12\,cm$$ radiates $$450\,watt$$ power at $$500\,K.$$ If the radius were halved and the temperature doubled, the power radiated in watt would be
A
225
B
450
C
1000
D
1800
Answer :
1800
60.
At what temperature will the resistance of a copper wire becomes three times its value at $${0^ \circ }C?$$
(Temperature coefficient of resistance of copper is $$4 \times {10^{ - 3}}{/^ \circ }C$$ )
A
$${550^ \circ }C$$
B
$${500^ \circ }C$$
C
$${450^ \circ }C$$
D
$${400^ \circ }C$$
Answer :
$${500^ \circ }C$$