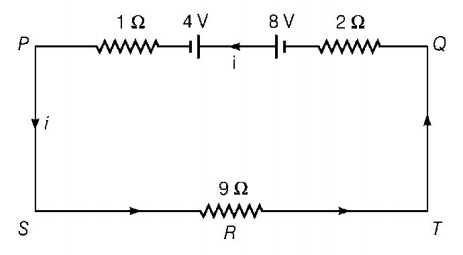
81.

In the circuit shown, the current through the $$4\,\Omega $$ resistor is $$1\,A$$ when the points $$P$$ and $$M$$ are connected to a DC voltage source. The potential difference between the points $$M$$ and $$N$$ is
A
$$1.5\,V$$
B
$$1.0\,V$$
C
$$0.5\,V$$
D
$$3.2\,V$$
Answer :
$$3.2\,V$$
82. If the cold junction of a thermocouple is kept at $${0^ \circ }C$$ and the hot junction is kept at $${T^ \circ }C,$$ then the relation between neutral temperature $$\left( {{T_n}} \right)$$ and temperature of inversion $$\left( {{T_i}} \right)$$ is
A
$${T_n} = \frac{{{T_i}}}{2}$$
B
$${T_n} = 2{T_i}$$
C
$${T_n} = {T_i} - T$$
D
$${T_n} = {T_i} + T$$
Answer :
$${T_n} = \frac{{{T_i}}}{2}$$
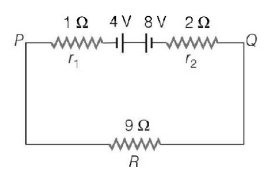
83.
Two batteries of emf $$4\,V$$ and $$8\,V$$ with internal resistance $$1\,\Omega $$ and $$2\,\Omega $$ are connected in a circuit with a resistance of $$9\,\Omega $$ as shown in figure. The current and potential difference between the points $$P$$ and $$Q$$ are
A
$$\frac{1}{3}A\,{\text{and}}\,3\,V$$
B
$$\frac{1}{6}A\,{\text{and}}\,4\,V$$
C
$$\frac{1}{9}A\,{\text{and}}\,9\,V$$
D
$$\frac{1}{{12}}A\,{\text{and}}\,12\,V$$
Answer :
$$\frac{1}{3}A\,{\text{and}}\,3\,V$$
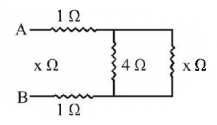
84.
The equivalent resistance between points $$A$$ and $$B$$ is

A
$$2R$$
B
$$\left( {\frac{3}{4}} \right)R$$
C
$$\left( {\frac{4}{3}} \right)R$$
D
$$\left( {\frac{3}{5}} \right)R$$
Answer :
$$\left( {\frac{3}{5}} \right)R$$
85. If the resistance of a conductor is $$5\,\Omega $$ at $${50^ \circ }C$$ and $$7\,\Omega $$ at $${100^ \circ }C,$$ then the mean temperature coefficient of resistance (of the material) is
A
$$0.01{/^ \circ }C$$
B
$$0.04{/^ \circ }C$$
C
$$0.06{/^ \circ }C$$
D
$$0.08{/^ \circ }C$$
Answer :
$$0.01{/^ \circ }C$$
86.
In Fig. find the value of resistor to be connected between $$C$$ and $$D,$$ so that the resistance of the entire circuit between $$A$$ and $$B$$ does not change with the number of elementary sets.

A
$$R$$
B
$$R\left( {\sqrt 3 - 1} \right)$$
C
$$3\,R$$
D
$$R\left( {\sqrt 3 + 1} \right)$$
Answer :
$$R\left( {\sqrt 3 - 1} \right)$$
87. A piece of copper and another of germanium are cooled from room temperature to $${80^ \circ }K.$$ The resistance of
A
each of them increases
B
each of them decreases
C
copper increases and germanium decreases
D
copper decreases and germanium increases
Answer :
copper decreases and germanium increases
88. In a meter bridge experiment null point is obtained at $$20\,cm.$$ from one end of the wire when resistance $$X$$ is balanced against another resistance $$Y.$$ If $$X < Y,$$ then where will be the new position of the null point from the same end, if one decides to balance a resistance of 4 $$X$$ against $$Y$$
A
$$40\,cm$$
B
$$80\,cm$$
C
$$50\,cm$$
D
$$70\,cm$$
Answer :
$$50\,cm$$
89.
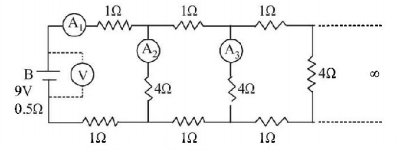
A $$9\,V$$ battery with internal resistance of $$0.5\,\Omega $$ is connected across an infinite network as shown in the figure. All ammeters $${A_1},{A_2},{A_3}$$ and voltmeter $$V$$ are ideal.
Choose correct statement.
A
Reading of $${A_1}$$ is $$2\,A$$
B
Reading of $${A_1}$$ is $$18\,A$$
C
Reading of $$V$$ is $$9\,V$$
D
Reading of $$V$$ is $$7\,V$$
Answer :
Reading of $${A_1}$$ is $$2\,A$$
90. An electric kettle takes $$4\,A$$ current at $$220\,V.$$ How much time will it take to boil $$1\,kg$$ of water from temperature $${20^ \circ }C$$ ?
A
$$6.3\,\min $$
B
$$8.4\,\min $$
C
$$12.6\,\min $$
D
$$4.2\,\min $$
Answer :
$$6.3\,\min $$