11.
The potential difference $$\left( {{V_A} - {V_B}} \right)$$ between the points $$A$$ and $$B$$ in the given figure is

A
$$ - 3\,V$$
B
$$ + 3\,V$$
C
$$ + 6\,V$$
D
$$ + 9\,V$$
Answer :
$$ + 9\,V$$
12. A heating coil is labelled $$100\,W,220\,V.$$ The coil is cut in two equal halves and the two pieces are joined in parallel to the same source. The energy now liberated per second is
A
$$25\,J$$
B
$$50\,J$$
C
$$200\,J$$
D
$$400\,J$$
Answer :
$$400\,J$$
13. A wire has a resistance $$12\,\Omega .$$ It is bent in the form of a circle. The effective resistance between two points on any diameter is
A
$$6\,\Omega $$
B
$$3\,\Omega $$
C
$$12\,\Omega $$
D
$$24\,\Omega $$
Answer :
$$3\,\Omega $$
14. Two voltameters, one of copper and another of silver, are joined in parallel. When a total charge $$q$$ flows through the voltameters, equal amount of metals are deposited. If the electrochemical equivalents of copper and silver are $${Z_1}$$ and $${Z_2}$$ respectively the charge which flows through the silver voltameter is
A
$$\frac{q}{{1 + \frac{{{Z_2}}}{{{Z_1}}}}}$$
B
$$\frac{q}{{1 + \frac{{{Z_1}}}{{{Z_2}}}}}$$
C
$$q\frac{{{Z_2}}}{{{Z_1}}}$$
D
$$q\frac{{{Z_1}}}{{{Z_2}}}$$
Answer :
$$\frac{q}{{1 + \frac{{{Z_2}}}{{{Z_1}}}}}$$
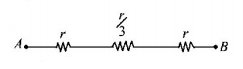
15.
In the network shown in figure each resistance is $$1\,\Omega .$$ The effective resistance between $$A$$ and $$B$$ is

A
$$\frac{4}{3}\Omega $$
B
$$\frac{3}{2}\Omega $$
C
$$7\,\Omega $$
D
$$\frac{8}{7}\Omega $$
Answer :
$$\frac{8}{7}\Omega $$
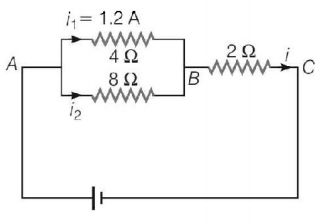
16.
In the circuit of figure, the current in $$4\,\Omega $$ resistance is $$1.2\,A,$$ what is the potential difference between $$B$$ and $$C$$ ?

A
$$3.6\,V$$
B
$$6.3\,V$$
C
$$1.8\,V$$
D
$$2.4\,V$$
Answer :
$$3.6\,V$$
17. Kirchhoff ’s first law of electricity follows
A
only law of conservation of energy
B
only law of conservation of charge
C
law of conservation of both energy and charge
D
sometimes law of conservation of energy and some other times law of conservation of charge
Answer :
only law of conservation of charge
18. An electric fan and a heater are marked as $$100\,W, 220\,V$$ and $$1000\,W, 220\,V$$ respectively. The resistance of heater is
A
equal to that of fan
B
lesser than that of fan
C
greater than that of fan
D
zero
Answer :
lesser than that of fan
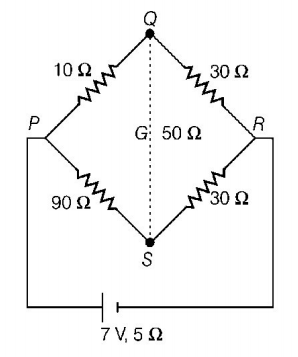
19. The resistances of the four arms $$P,Q,R$$ and $$S$$ in a Wheatstone bridge are $$10\,\Omega ,30\,\Omega ,30\,\Omega $$ and $$90\,\Omega ,$$ respectively. The emf and internal resistance of the cell are $$7\,V$$ and $$5\,\Omega $$ respectively. If the galvanometer resistance is $$50\,\Omega ,$$ the current drawn from the cell will be
A
$$1.0\,A$$
B
$$0.2\,A$$
C
$$0.1\,A$$
D
$$2.0\,A$$
Answer :
$$0.2\,A$$
20.
All wires have same resistance and equivalent resistance between $$A$$ and $$B$$ is $${R_0}.$$ Now keys are closed, then the equivalent resistance will become
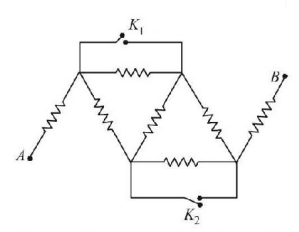
A
$$\frac{{7\,{R_0}}}{3}$$
B
$$\frac{{7\,{R_0}}}{9}$$
C
$${7\,{R_0}}$$
D
$$\frac{{{R_0}}}{3}$$
Answer :
$$\frac{{7\,{R_0}}}{9}$$