31.
Find out the value of current through $$2\Omega $$ resistance for the given circuit.

A
zero
B
$$2A$$
C
$$5A$$
D
$$4A$$
Answer :
zero
32. A moving coil galvanometer has 150 equal divisions. Its current sensitivity is 10-divisions per milliampere and voltage sensitivity is 2 divisions per milli volt. In order that each division reads $$1\,volt,$$ the resistance in ohms needed to be connected in series with the coil will be -
A
$${10^5}$$
B
$${10^3}$$
C
$$9995$$
D
$$99995$$
Answer :
$$9995$$
33. In an ammeter $$0.2\% $$ of main current passes through the galvanometer. If resistance battery of galvanometer is $$G,$$ the resistance of ammeter will be
A
$$\frac{1}{{499}}G$$
B
$$\frac{{499}}{{500}}G$$
C
$$\frac{1}{{500}}G$$
D
$$\frac{{500}}{{499}}G$$
Answer :
$$\frac{1}{{500}}G$$
34.
From the graph between current $$I$$ and voltage $$V$$ shown in figure, identify the portion corresponding to negative resistance.

A
$$DE$$
B
$$CD$$
C
$$BC$$
D
$$AB$$
Answer :
$$CD$$
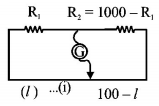
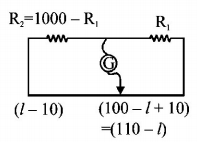
35. On interchanging the resistances, the balance point of a meter bridge shifts to the left by $$10\,cm.$$ The resistance of their series combination is $$1k\,\Omega $$. How much was the resistance on the left slot before interchanging the resistances?
A
$$990\,\Omega $$
B
$$505\,\Omega $$
C
$$550\,\Omega $$
D
$$910\,\Omega $$
Answer :
$$550\,\Omega $$
36. A potentiometer consists of a wire of length $$4\,m$$ and resistance $$10\,\Omega .$$ It is connected to a cell of emf $$2\,V.$$ The potential gradient of the wire is
A
$$0.5\,V/m$$
B
$$2\,V/m$$
C
$$5\,V/m$$
D
$$10\,V/m$$
Answer :
$$0.5\,V/m$$
37.
Shown in figure is a Post Office box. In order to calculate the value of external resistance, it should be connected between

A
$$B'$$ and $$C$$
B
$$A$$ and $$D$$
C
$$C$$ and $$D$$
D
$$B$$ and $$D$$
Answer :
$$A$$ and $$D$$
38. You are given several identical resistances each of value $$R = 10\,\Omega $$ and each capable of carrying a maximum current of $$1\,A.$$ It is required to make a suitable combination of these resistances of $$5\,\Omega $$ which can carry a current of $$4\,A.$$ The minimum number of resistances of the type $$R$$ that will be required for this job is
A
4
B
10
C
8
D
20
Answer :
8
39. An electron beam has an aperture $$1.0\,m{m^2}.$$ A total of $$6 \times {10^{16}}$$ electrons go through any perpendicular cross section per second. Find the current density in the beam. (in $$A/{m^2}$$ )
A
$$9.1 \times {10^{13}}$$
B
$$9.6 \times {10^3}$$
C
$$6.6 \times {10^5}$$
D
$$8.6 \times {10^{11}}$$
Answer :
$$9.6 \times {10^3}$$
40. The thermo emf of a thermocouple varies with the temperature $$\theta $$ of the hot junction as $$E = a\theta + b{\theta ^2}$$ in volts where the ratio $$\frac{a}{b}$$ is $${700^ \circ }C.$$ If the cold junction is kept at $${0^ \circ }C,$$ then the neutral temperature is
A
$${1400^ \circ }C$$
B
$${350^ \circ }C$$
C
$${700^ \circ }C$$
D
No neutral temperature is possible for this termocouple.
Answer :
No neutral temperature is possible for this termocouple.