131.
A wire of resistance 12 ohms per meter is bent to form a complete circle of radius $$10\,cm.$$ The resistance between its two diametrically opposite points, $$A$$ and $$B$$ as shown in the figure, is

A
$$3\Omega $$
B
$$6\pi \Omega $$
C
$$6\Omega $$
D
$$0.6\pi \Omega $$
Answer :
$$3\Omega $$
132. Water boils in the electric kettle in 15 minutes after switching on. If the length of heating wire is decreased to $$\frac{2}{3}$$ of its initial value, then the same amount of water will boil with the same supply voltage in
A
8 minutes
B
10 minutes
C
12 minutes
D
15 minutes
Answer :
10 minutes
133. Cell having an emf $$\varepsilon $$ and internal resistance $$r$$ is connected across a variable external resistance $$R.$$ As the resistance $$R$$ is increased, the plot of potential difference $$V$$ across $$R$$ is given by :
A


B


C


D


Answer :


134. The number of free electrons per $$100\,mm$$ of ordinary copper wire is $$2 \times {10^{21}}.$$ Average drift speed of electrons is $$0.25\,mm/s.$$ The current flowing is
A
$$5\,A$$
B
$$80\,A$$
C
$$8\,A$$
D
$$0.8\,A$$
Answer :
$$0.8\,A$$
135. In a metre bridge, the balancing length from the left end (standard resistance of one ohm is in the right gap) is found to be $$20\,cm.$$ The value of the unknown resistance is
A
$$0.8\,\Omega $$
B
$$0.5\,\Omega $$
C
$$0.4\,\Omega $$
D
$$0.25\,\Omega $$
Answer :
$$0.25\,\Omega $$
136. Suppose the drift velocity $${v_d}$$ in a material varied with the applied electric field $$E$$ as $${v_d} \propto \sqrt E .$$ Then $$V-I$$ graph for a wire made of such a material is best given by :
A


B


C


D


Answer :


137. Two wires of the same metal have same length, but their cross-sections are in the ratio $$3:1.$$ They are joined in series. The resistance of thicker wire is $$10\,\Omega .$$ The total resistance of the combination will be
A
$$10\,\Omega $$
B
$$20\,\Omega $$
C
$$40\,\Omega $$
D
$$100\,\Omega $$
Answer :
$$40\,\Omega $$
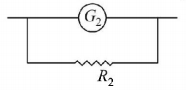
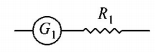
138. To verify Ohm’s law, a student is provided with a test resistor $${R_T},$$ a high resistance $${R_1},$$ a small resistance $${R_2},$$ two identical galvanometers $${G_1}$$ and $${G_2,}$$ and a variable voltage source $$V.$$ The correct circuit to carry out the experiment is
A


B


C


D


Answer :


139. If voltage across a bulb rated $$220\,V - 100\,W$$ drops by $$2.5\% $$ of its rated value, the percentage of the rated value by which the power would decrease is
A
$$20\% $$
B
$$2.5\% $$
C
$$5\% $$
D
$$10\% $$
Answer :
$$5\% $$
140.
A 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current $$I,$$ in the circuit will be

A
$$1A$$
B
$$1.5A$$
C
$$2A$$
D
$$\frac{1}{3}A$$
Answer :
$$1.5A$$