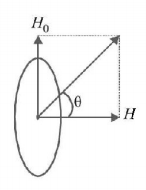
101. A current carrying coil is placed with its axis perpendicular to $$N-S$$ direction. Let horizontal component of earth’s magnetic field be $${H_0}$$ and magnetic field inside the loop be $$H.$$ If a magnet is suspended inside the loop, it makes angle $$\theta $$ with $$H.$$ Then $$\theta = $$
A
$${\tan ^{ - 1}}\left( {\frac{{{H_0}}}{H}} \right)$$
B
$${\tan ^{ - 1}}\left( {\frac{H}{{{H_0}}}} \right)$$
C
$${\text{cose}}{{\text{c}}^{ - 1}}\left( {\frac{H}{{{H_0}}}} \right)$$
D
$${\cot ^{ - 1}}\left( {\frac{{{H_0}}}{H}} \right)$$
Answer :
$${\tan ^{ - 1}}\left( {\frac{{{H_0}}}{H}} \right)$$
102.
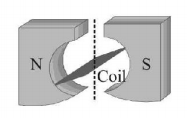
The figure below shows the north and south poles of a permanent magnet in which n turn coil of area of cross-section $$A$$ is resting, such that for a current $$i$$ passed through the coil, the plane of the coil makes an angle $$\theta $$ with respect to the direction of magnetic field $$B.$$ If the plane of the magnetic field and the coil are horizontal and vertical respectively, the torque on the coil will be
A
$$\tau = niAB\cos \theta $$
B
$$\tau = niAB\sin \theta $$
C
$$\tau = niAB$$
D
None of the above, since the magnetic field is radial
Answer :
$$\tau = niAB\cos \theta $$
103. Two short magnets with their axes horizontal and perpendicular to the magnetic maridian are placed with their centres $$40\,cm$$ east and $$50\,cm$$ west of magnetic needle. If the needle remains undeflected, the ratio of their magnetic moments $${M_1}:{M_2}$$ is
A
$$4:5$$
B
$$16:25$$
C
$$64:125$$
D
$$2:\sqrt 5 $$
Answer :
$$64:125$$
104. If the magnetic dipole moment of an atom of diamagnetic material, paramagnetic material and ferromagnetic material are denoted by $${\mu _d},{\mu _p}$$ and $${\mu _f}$$ respectively, then
A
$${\mu _d} \ne 0\,{\text{and}}\,{\mu _f} \ne 0$$
B
$${\mu _p} = 0\,{\text{and}}\,{\mu _f} \ne 0$$
C
$${\mu _d} = 0\,{\text{and}}\,{\mu _p} \ne 0$$
D
$${\mu _d} \ne 0\,{\text{and}}\,{\mu _p} = 0$$
Answer :
$${\mu _d} = 0\,{\text{and}}\,{\mu _p} \ne 0$$
105. A very small magnet is placed in the magnetic meridian with its south pole pointing north. The null point is obtained $$20\,cm$$ away from the centre of the magnet. If the earth’s magnetic field (horizontal component) at this point be $$0.3\,gauss,$$ the magnetic moment of the magnet is
A
$$8.0 \times {10^2}\,e.m.u.$$
B
$$1.2 \times {10^3}\,e.m.u.$$
C
$$2.4 \times {10^3}\,e.m.u.$$
D
$$3.6 \times {10^3}\,e.m.u.$$
Answer :
$$1.2 \times {10^3}\,e.m.u.$$
106. Two bar magnets having same geometry with magnetic moments $$M$$ and $$2M,$$ are firstly placed in such a way that their similar poles are on the same side, then its period of oscillation is $${T_1}.$$ Now, the polarity of one of the magnets is reversed the time period of oscillations becomes $${T_2}.$$ Then,
A
$${T_1} < {T_2}$$
B
$${T_1} > {T_2}$$
C
$${T_1} = {T_2}$$
D
$${T_2} = \infty $$
Answer :
$${T_1} < {T_2}$$