71. A bar magnet of magnetic moment $$3.0\,A{\text{ - }}{m^2}$$ is placed in a uniform magnetic field of $$2 \times {10^{ - 5}}T.$$ If each pole of the magnet experiences a force of $$6 \times {10^{ - 4}}N,$$ the length of the magnet is
A
$$0.5\,m$$
B
$$0.3\,m$$
C
$$0.2\,m$$
D
$$0.1\,m$$
Answer :
$$0.1\,m$$
72. The magnetic needle of a tangent galvanometer is deflected at an angle $${30^ \circ }$$ due to a magnet. The horizontal component of earth's magnetic field $$0.34 \times {10^{ - 4}}T$$ is along the plane of the coil. The magnetic intensity is
A
$$1.96 \times {10^{ - 4}}T$$
B
$$1.96 \times {10^{ - 5}}T$$
C
$$1.96 \times {10^{ 4}}T$$
D
$$1.96 \times {10^{5}}T$$
Answer :
$$1.96 \times {10^{ - 5}}T$$
73. The magnetic susceptibility of a paramagnetic substances at $$ - {73^ \circ }C$$ is $$0.0060,$$ then its value at $$ - {173^ \circ }C$$ will be
A
0.0030
B
0.0120
C
0.0180
D
0.0045
Answer :
0.0120
74. A vibration magnetometer consists of two identical bar magnets placed one over the other such that they are perpendicular and bisect each other. The time period of oscillation in a horizontal magnetic field is $${2^{\frac{5}{4}}}{\text{seconds}}.$$ One of the magnets is removed and if the other magnet oscillates in the same field, then the time period in seconds is
A
$${2^{\frac{1}{4}}}$$
B
$${2^{\frac{1}{2}}}$$
C
$$2$$
D
$${2^{\frac{3}{4}}}$$
Answer :
$$2$$
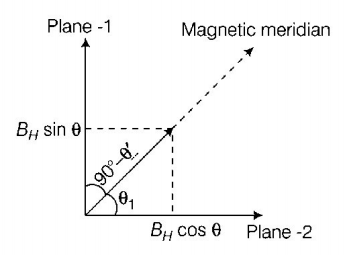
76. If $${\theta _1}$$ and $${\theta _2}$$ be the apparent angles of dip observed in two vertical planes at right angles to each other, then the true angle of dip $$\theta $$ is given by
A
$${\cot ^2}\theta = {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2}$$
B
$${\tan ^2}\theta = {\tan ^2}{\theta _1} + {\tan ^2}{\theta _2}$$
C
$${\cot ^2}\theta = {\cot ^2}{\theta _1} - {\cot ^2}{\theta _2}$$
D
$${\tan ^2}\theta = {\tan ^2}{\theta _1} - {\tan ^2}{\theta _2}$$
Answer :
$${\cot ^2}\theta = {\cot ^2}{\theta _1} + {\cot ^2}{\theta _2}$$
77. Relative permeability of iron is $$5500,$$ then its magnetic susceptibility will be
A
$$5501$$
B
$$5499$$
C
$$5500 \times {10^7}$$
D
None of these
Answer :
$$5499$$
78. A magnet of magnetic moment $$M$$ is rotated through $${360^ \circ }$$ in a magnetic field $$H,$$ the work done will be
A
$$MH$$
B
$$2MH$$
C
$$2\pi MH$$
D
Zero
Answer :
Zero
79. The magnetic needle has magnetic moment $$8.7 \times {10^{ - 2}}A{m^2}$$ and moment of inertia $$11.5 \times {10^{ - 6}}\,kg{m^2}.$$ It performs 10 complete oscillations in $$6.70\,s,$$ what is the magnitude of the magnetic field?
A
$$0.012\,T$$
B
$$0.120\,T$$
C
$$1.200\,T$$
D
$$2.10\,T$$
Answer :
$$0.012\,T$$
80. Curie temperature is the temperature above which
A
a ferromagnetic material becomes paramagnetic
B
a paramagnetic material becomes diamagnetic
C
a ferromagnetic material becomes diamagnetic
D
a paramagnetic material becomes ferromagnetic
Answer :
a ferromagnetic material becomes paramagnetic