21. A long solenoid carrying a current produces a magnetic field $$B$$ along its axis. If the current is doubled and the number of turns per $$cm$$ is halved, the new value of the magnetic field is
A
$$2B$$
B
$$4B$$
C
$$\frac{B}{2}$$
D
$$B$$
Answer :
$$B$$
22.
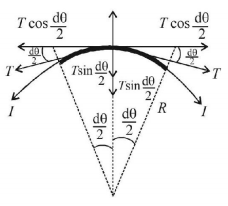
A thin flexible wire of length $$L$$ is connected to two adjacent fixed points and carries a current $$I$$ in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength $$B$$ going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is
A
$$IBL$$
B
$$\frac{{IBL}}{\pi }$$
C
$$\frac{{IBL}}{{2\pi }}$$
D
$$\frac{{IBL}}{{4\pi }}$$
Answer :
$$\frac{{IBL}}{{2\pi }}$$
23. The orbital speed of electron orbiting around a nucleus in a circular orbit of radius $$50\,pm$$ is $$2.2 \times {10^6}\,m{s^{ - 1}}.$$ Then the magnetic dipole moment of an electron is
A
$$1.6 \times {10^{ - 19}}A{m^2}$$
B
$$5.3 \times {10^{ - 21}}A{m^2}$$
C
$$8.8 \times {10^{ - 25}}A{m^2}$$
D
$$8.8 \times {10^{ - 26}}A{m^2}$$
Answer :
$$8.8 \times {10^{ - 25}}A{m^2}$$
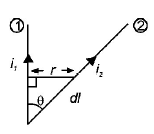
24.
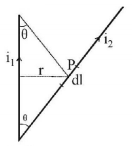
Wires 1 and 2 carrying currents $${i_1}$$ and $${i_2}$$ respectively are inclined at an angle $$\theta $$ to each other. What is the force on a small element $$dl$$ of wire 2 at a distance of $$r$$ from wire 1 (as shown in figure) due to the magnetic field of wire 1?
A
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\tan \theta $$
B
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\sin \theta $$
C
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\cos \theta $$
D
$$\frac{{{\mu _0}}}{{4\pi r}}{i_1}{i_2}dl\sin \theta $$
Answer :
$$\frac{{{\mu _0}}}{{2\pi r}}{i_1}{i_2}dl\cos \theta $$
25. A straight wire of diameter $$0.5\,mm$$ carrying a current of $$1\,A$$ is replaced by another wire of $$1\,mm$$ diameter carrying same current. The strength of magnetic field far away is
A
twice the earlier value
B
same as the earlier value
C
one-half of the earlier value
D
one-quarter of the earlier value
Answer :
same as the earlier value
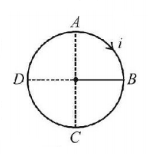
26.
A circular coil $$ABCD$$ carrying a current $$i$$ is placed in a uniform magnetic field. If the magnetic force on the segment $$AB$$ is $$\vec F,$$ the force on the remaining segment $$BCDA$$ is
A
$${\vec F}$$
B
$$ - \vec F$$
C
$$3\vec F$$
D
$$ - 3\vec F$$
Answer :
$$ - \vec F$$
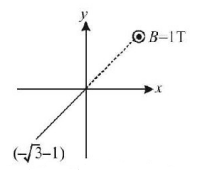
27.
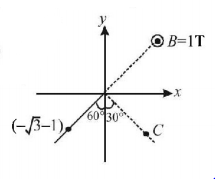
A uniform magnetic field of magnitude $$1\,T$$ exists in region $$y \geqslant 0$$ is along $${\hat k}$$ direction as shown. A particle of charge $$1\,C$$ is projected from point $$\left( { - \sqrt 3 , - 1} \right)$$ towards origin with speed $$1\,m/\sec.$$ If mass of particle is $$1\,kg,$$ then co-ordinates of centre of circle in which particle moves are -
A
$$\left( {1,\sqrt 3 } \right)$$
B
$$\left( {1, - \sqrt 3 } \right)$$
C
$$\left( {\frac{1}{2}, - \frac{{\sqrt 3 }}{2}} \right)$$
D
$$\left( {\frac{{\sqrt 3 }}{2}, - \frac{1}{2}} \right)$$
Answer :
$$\left( {\frac{1}{2}, - \frac{{\sqrt 3 }}{2}} \right)$$
28. The magnetic field due to a current carrying circular loop of radius $$3cm$$ at a point on the axis at a distance of $$4cm$$ from the centre is 54 $$\mu T.$$ What will be its value at the centre of loop?
A
$$125\mu T$$
B
$$150\mu T$$
C
$$250\mu T$$
D
$$75\mu T$$
Answer :
$$250\mu T$$
29. A current carrying conductor placed in a magnetic field experiences maximum force when angle between current and magnetic field is
A
$$\frac{{3\,\pi }}{4}$$
B
$$\frac{\pi }{2}$$
C
$$\frac{\pi }{4}$$
D
zero
Answer :
$$\frac{\pi }{2}$$
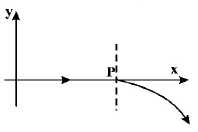
30.
For a positively charged particle moving in a $$x-y$$ plane initially along the $$x$$-axis, there is a sudden change in its path due to the presence of electric and/or magnetic fields beyond $$P.$$ The curved path is shown in the $$x-y$$ plane and is found to be non-circular. Which one of the following combinations is possible?
A
$$\overrightarrow E = 0;\,\overrightarrow B = b\hat i + c\hat k$$
B
$$\overrightarrow E = a\hat i;\,\overrightarrow B = c\hat k + a\hat i$$
C
$$\overrightarrow E = 0;\,\overrightarrow B = c\hat j + b\hat k$$
D
$$\overrightarrow E = a\hat i;\,\overrightarrow B = c\hat k + b\hat j$$
Answer :
$$\overrightarrow E = a\hat i;\,\overrightarrow B = c\hat k + a\hat i$$