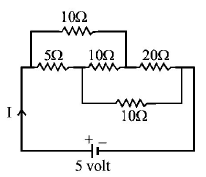
111.
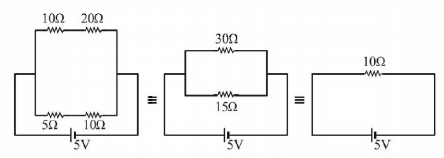
The current $$I$$ drawn from the $$5\,volt$$ source will be
A
$$0.33\,A$$
B
$$0.5\,A$$
C
$$0.67\,A$$
D
$$0.17\,A$$
Answer :
$$0.5\,A$$
112.
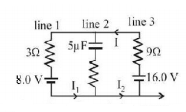
The circuit shown here has two batteries of $$8.0\,V$$ and $$16.0\,V$$ and three resistors $$3\,\Omega ,9\,\Omega $$ and $$9\,\Omega $$ and a capacitor of $$5.0\,\mu F.$$
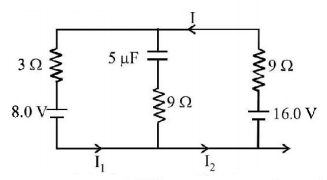
How much is the current $$I$$ in the circuit in steady state?
A
$$1.6\,A$$
B
$$0.67\,A$$
C
$$2.5\,A$$
D
$$0.25\,A$$
Answer :
$$0.67\,A$$
113.
This questions has Statement I and Statement II. Of the four choices given after the Statements, choose the one that best describes into two Statements.
Statement-I : Higher the range, greater is the resistance of ammeter.
Statement-II : To increase the range of ammeter, additional shunt needs to be used across it.
A
Statement-I is true, Statement-II is true, Statement-II is the correct explanation of Statement-I.
B
Statement-I is true, Statement-II is true, Statement-II is not the correct explanation of Statement-I.
C
Statement-I is true, Statement-II is false.
D
Statement-I is false, Statement-II is true.
Answer :
Statement-I is false, Statement-II is true.
114.
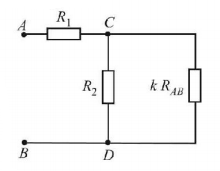
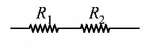
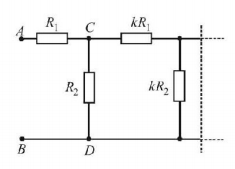
The circuit diagram shown in figure consists of a very large (infinite) number of elements. resistances of the resistors in each subsequent element differ by a factor of $$k$$ from the resistances of the resistors in the previous elements. Determine the resistance $${R_{AB}}$$ between points $$A$$ and $$B$$ if the resistances of the first element are $${R_1}$$ and $${R_2}.\left( {k = \frac{1}{2}} \right)$$
A
$$\frac{{{R_1} - {R_2} + \sqrt {R_1^2 + R_2^2 + 6{R_1}{R_2}} }}{2}$$
B
$$\frac{{{R_1} + {R_2} + \sqrt {R_1^2 + R_2^2 + 6{R_1}{R_2}} }}{2}$$
C
$$\frac{{{R_1} - {R_2} - \sqrt {R_1^2 + R_2^2 + 6{R_1}{R_2}} }}{2}$$
D
None of these
Answer :
$$\frac{{{R_1} - {R_2} + \sqrt {R_1^2 + R_2^2 + 6{R_1}{R_2}} }}{2}$$
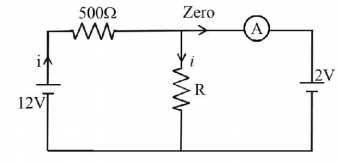
115.
In the circuit , the galvanometer $$G$$ shows zero deflection. If the batteries $$A$$ and $$B$$ have negligible internal resistance, the value of the resistor $$R$$ will be -
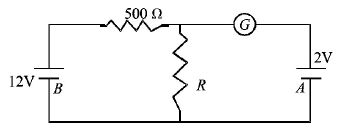
A
$$100\Omega $$
B
$$200\Omega $$
C
$$1000\Omega $$
D
$$500\Omega $$
Answer :
$$100\Omega $$
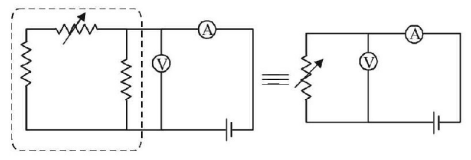
116. Express which of the following set ups can be used to verify Ohm’s law?
A
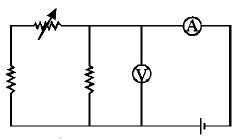

B
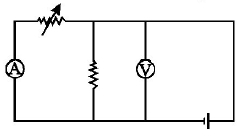

C
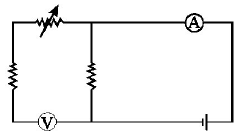

D
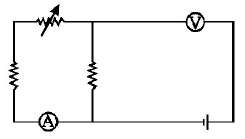

Answer :


117. The resistance of the series combination of two resistances is $$S.$$ when they are joined in parallel the total resistance is $$P.$$ If $$S = nP$$ then the Minimum possible value of $$n$$ is
A
2
B
3
C
4
D
1
Answer :
4
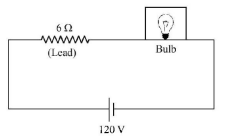
118. The supply voltage to room is $$120V.$$ The resistance of the lead wires is $$6\Omega .A\,60 W$$ bulb is already switched on. What is the decrease of voltage across the bulb, when a $$240\,W$$ heater is switched on in parallel to the bulb?
A
zero
B
$$2.9\,Volt$$
C
$$13.3\,Volt$$
D
$$10.04\,Volt$$
Answer :
$$10.04\,Volt$$
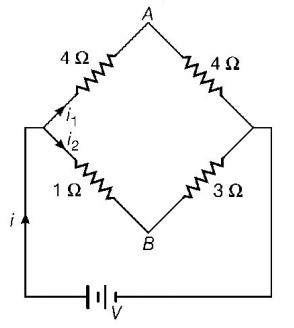
119.
In the circuit shown, if a conducting wire is connected between points $$A$$ and $$B,$$ the current in this wire will
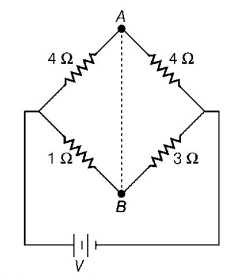
A
flow from $$A$$ to $$B$$
B
flow in the direction which will be decided by the value of $$V$$
C
be zero
D
flow from $$B$$ to $$A$$
Answer :
flow from $$B$$ to $$A$$
120.
The resistances in the two arms of the meter bridge are $$5\Omega $$ and $$R\Omega ,$$ respectively. When the resistance $$R$$ is shunted with an equal resistance, the new balance point is at $$1.6\,{l_1}.$$ The resistance $$'R'$$ is:
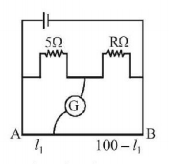
A
$$10\Omega $$
B
$$15\Omega $$
C
$$20\Omega $$
D
$$25\Omega $$
Answer :
$$15\Omega $$