171. Resistivity of potentiometer wire is $${10^{ - 7}}\Omega - m$$ and its area of cross-section is $${10^{ - 6}}{m^2}.$$ When a current $$i = 0.1\,A$$ flows through the wire, its potential gradient is
A
$${10^{ - 2}}V/m$$
B
$${10^{ - 4}}V/m$$
C
$$0.1\,V/m$$
D
$$10\,V/m$$
Answer :
$${10^{ - 2}}V/m$$
172. A electric tea kettle has two heating coils. When first coil of resistance $${R_1}$$ is switched on, the kettle begins to boil tea in 6 minutes. When second coil of resistance $${R_2}$$ is switched on, the boiling begins in 8 minutes. The value of $$\frac{{{R_1}}}{{{R_2}}}$$ is
A
$$\frac{7}{3}$$
B
$$\frac{3}{7}$$
C
$$\frac{3}{4}$$
D
$$\frac{4}{3}$$
Answer :
$$\frac{3}{4}$$
173. A wire of resistance $$4\,\Omega $$ is stretched to twice its original length. The resistance of stretched wire would be
A
$$2\,\Omega $$
B
$$4\,\Omega $$
C
$$8\,\Omega $$
D
$$16\,\Omega $$
Answer :
$$16\,\Omega $$
174. If nearly $${10^5}C$$ liberate $$1\,g$$ equivalent of aluminium, then the amount of aluminium (equivalent weight 9) deposited through electrolysis in $$20\,min$$ by a current of $$50\,A$$ will be
A
$$0.6\,g$$
B
$$0.09\,g$$
C
$$5.4\,g$$
D
$$10.8\,g$$
Answer :
$$5.4\,g$$
175. The charge following through a resistance $$R$$ varies with time $$t$$ as $$Q = at - b{t^2},$$ where $$a$$ and $$b$$ are positive constants. The total heat produced in $$R$$ is
A
$$\frac{{{a^3}R}}{{3b}}$$
B
$$\frac{{{a^3}R}}{{2b}}$$
C
$$\frac{{{a^3}R}}{b}$$
D
$$\frac{{{a^3}R}}{{6b}}$$
Answer :
$$\frac{{{a^3}R}}{{6b}}$$
176.
A $$100\,W$$ bulb $${B_1}$$ and two $$60\,W$$ bulb $${B_2}$$ and $${B_3},$$ are connected to a $$250\,V$$ source, as shown in figure. Now $${W_1},{W_2}$$ and $${W_3}$$ are the output powers of the bulbs $${B_1},{B_2}$$ and $${B_3},$$ respectively. Then
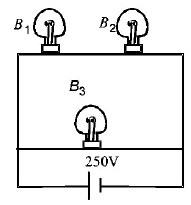
A
$${W_1} > {W_2} = {W_3}$$
B
$${W_1} > {W_2} > {W_3}$$
C
$${W_1} < {W_2} = {W_3}$$
D
$${W_1} < {W_2} < {W_3}$$
Answer :
$${W_1} < {W_2} < {W_3}$$
177. Two cities are $$150\,km$$ apart. Electric power is sent from one city to another city through copper wires. The fall of potential per $$km$$ is $$8\,V$$ and the average resistance per $$km$$ is $$0.5\,\Omega .$$ The power loss in the wire is
A
$$19.2\,W$$
B
$$19.2\,kW$$
C
$$19.2\,J$$
D
$$12.2\,kW$$
Answer :
$$19.2\,kW$$
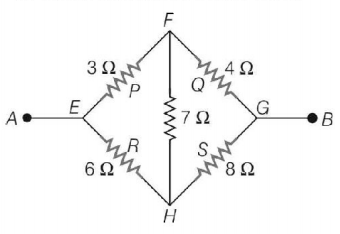
178.
A bridge circuit is shown in figure. The equivalent resistance between $$A$$ and $$B$$ will be

A
$$21\,\Omega $$
B
$$7\,\Omega $$
C
$$\frac{{252}}{{85}}\Omega $$
D
$$\frac{{14}}{3}\Omega $$
Answer :
$$\frac{{14}}{3}\Omega $$
179. Two sources of equal emf are connected to an external resistance $$R.$$ The internal resistance of the two sources are $${R_1}$$ and $${R_2}\left( {{R_1} > {R_1}} \right).$$ If the potential difference across the source having internal resistance $${R_2}$$ is zero, then
A
$$R = {R_2} - {R_1}$$
B
$$R = \frac{{{R_2} \times \left( {{R_1} + {R_2}} \right)}}{{\left( {{R_2} - {R_1}} \right)}}$$
C
$$R = \frac{{{R_1}{R_2}}}{{\left( {{R_2} - {R_1}} \right)}}$$
D
$$R = \frac{{{R_1}{R_2}}}{{\left( {{R_1} - {R_2}} \right)}}$$
Answer :
$$R = {R_2} - {R_1}$$
180. An electric kettle has two heating coils. When one of the coils is connected to an AC source, the water in the kettle boils in $$10\,min.$$ When the other coil is used the water boils in $$40\,min.$$ If both the coils are connected in parallel, the time taken by the same quantity of water to boil will be
A
$$25\,min$$
B
$$15\,min$$
C
$$8\,min$$
D
$$4\,min$$
Answer :
$$8\,min$$