71. A step-up transformer operates on a $$230\,V$$ line and supplies current of $$2\,A$$ to a load. The ratio of the primary and secondary windings is $$1:25.$$ The current in the primary coil is
A
$$15\,A$$
B
$$50\,A$$
C
$$25\,A$$
D
$$12.5\,A$$
Answer :
$$50\,A$$
72. In an electromagnetic wave in free space the root mean square value of the electric field is $${E_{{\text{rms}}}} = 6\,V/m.$$ The peak value of the magnetic field is
A
$$1.41 \times {10^{ - 8}}T$$
B
$$2.83 \times {10^{ - 8}}T$$
C
$$0.70 \times {10^{ - 8}}T$$
D
$$4.23 \times {10^{ - 8}}T$$
Answer :
$$2.83 \times {10^{ - 8}}T$$
73. A transformer having efficiency of $$90\% $$ is working on $$200\,V$$ and $$3\,kW$$ power supply. If the current in the secondary coil is $$6A,$$ the voltage across the secondary coil and the current in the primary coil respectively are :
A
$$300\,V,15\,A$$
B
$$450\,V,15\,A$$
C
$$450\,V,13.5\,A$$
D
$$600\,V,15\,A$$
Answer :
$$450\,V,15\,A$$
74.
As shown in figure, value of inductive reactance $${X_L}$$ will be if source voltage is 100 volt
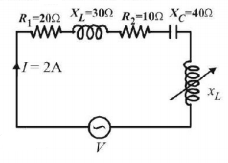
A
$$40\,\Omega $$
B
$$30\,\Omega $$
C
$$50\,\Omega $$
D
can have any value
Answer :
$$50\,\Omega $$
75.
When an $$AC$$ source of emf $$e = {E_0}\sin \left( {100t} \right)$$ is connected across a circuit, the phase difference between the emf $$e$$ and the current $$i$$ in the circuit is observed to be $$\frac{\pi }{4},$$ as shown in the diagram. If the circuit consists possibly only of $$R - C$$ or $$R - L$$ or $$L - C$$ in series, find the relationship between the two elements
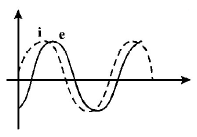
A
$$R = 1k\Omega ,C = 10\mu F$$
B
$$R = 1k\Omega ,C = 1\mu F$$
C
$$R = 1k\Omega ,L = 10H$$
D
$$R = 1k\Omega ,L = 1H$$
Answer :
$$R = 1k\Omega ,C = 10\mu F$$
76. A coil of inductance $$8.4\,mH$$ and resistance $$6\,\Omega $$ is connected to a $$12\,V$$ battery. The current in the coil is $$1.0\,A$$ at approximately the time
A
$$500\,s$$
B
$$25\,s$$
C
$$35\,ms$$
D
$$1\,ms$$
Answer :
$$1\,ms$$
77.
Find the current passing through battery immediately after key $$\left( K \right)$$ is closed. It is given that initially all the capacitors are uncharged.
(given that $$R = 6\,\Omega $$ and $$C = 4\mu F$$ )
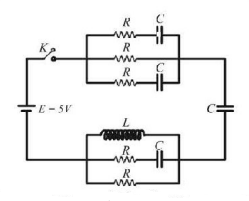
A
$$1\,A$$
B
$$5\,A$$
C
$$3\,A$$
D
$$2\,A$$
Answer :
$$1\,A$$
78. In a circuit, $$L,C$$ and $$R$$ are connected in series with an alternating voltage source of frequency $$f.$$ The current leads the voltage by $${45^ \circ }.$$ The value of $$C$$ is
A
$$\frac{1}{{2\pi f\left( {2\pi fL + R} \right)}}$$
B
$$\frac{1}{{\pi f\left( {2\pi fL + R} \right)}}$$
C
$$\frac{1}{{2\pi f\left( {2\pi fL - R} \right)}}$$
D
$$\frac{1}{{\pi f\left( {2\pi fL - R} \right)}}$$
Answer :
$$\frac{1}{{2\pi f\left( {2\pi fL - R} \right)}}$$
79. The voltage of an $$ac$$ supply varies with time $$\left( t \right)$$ as $$V = 120\sin 100\pi \,t\cos 100\,\pi t.$$ The maximum voltage and frequency respectively are
A
$$120\,volts,100\,Hz$$
B
$$\frac{{120}}{{\sqrt 2 }}volts,100\,Hz$$
C
$$60\,volts,200\,Hz$$
D
$$60\,volts,100\,Hz$$
Answer :
$$60\,volts,100\,Hz$$
80.
The voltage time $$\left( {V - t} \right)$$ graph for triangular wave having peak value $${V_0}$$ is as shown in figure. The $$rms$$ value of $$V$$ in time interval from $$t = 0$$ to $$\frac{T}{4}$$ is
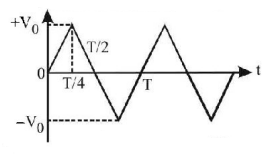
A
$$\frac{{{V_0}}}{{\sqrt 3 }}$$
B
$$\frac{{{V_0}}}{2}$$
C
$$\frac{{{V_0}}}{{\sqrt 2 }}$$
D
$$\frac{{{V_0}}}{3}$$
Answer :
$$\frac{{{V_0}}}{{\sqrt 3 }}$$