81. In an $$ac$$ circuit an alternating voltage $$e = 200\sqrt 2 \sin 100\,t\,{\text{volts}}$$ is connected to a capacitor of capacity $$1\,\mu F.$$ The $$r.m.s.$$ value of the current in the circuit is
A
$$10\,mA$$
B
$$100\,mA$$
C
$$200\,mA$$
D
$$20\,mA$$
Answer :
$$20\,mA$$
82. A 220 volts input is supplied to a transformer. The output circuit draws a current of $$2.0$$ ampere at $$440$$ volts. If the efficiency of the transformer is $$80\% ,$$ the current drawn by the primary windings of the transformer is
A
3.6 ampere
B
2.8 ampere
C
2.5 ampere
D
5.0 ampere
Answer :
5.0 ampere
83. In a series $$LCR$$ circuit $$R = 200\Omega $$ and the voltage and the frequency of the main supply is $$220V$$ and $$50 Hz$$ respectively. On taking out the capacitance from the circuit the current lags behind the voltage by $${30^ \circ }.$$ On taking out the inductor from the circuit the current leads the voltage by $${30^ \circ }.$$ The power dissipated in the $$LCR$$ circuit is
A
$$305 W$$
B
$$210 W$$
C
Zero $$W$$
D
$$242 W$$
Answer :
$$242 W$$
84. Alternating current can not be measured by $$D.C.$$ ammeter because
A
Average value of current for complete cycle is zero
B
$$A.C.$$ Changes direction
C
$$A.C.$$ can not pass through $$D.C.$$ Ammeter
D
$$D.C.$$ Ammeter will get damaged.
Answer :
Average value of current for complete cycle is zero
85. The primary of a transformer when connected to a $$dc$$ battery of $$10$$ volt draws a current of $$1\,mA.$$ The number of turns of the primary and secondary windings are $$50$$ and $$100$$ respectively. The voltage in the secondary and the current drawn by the circuit in the secondary are respectively
A
$$20\,V$$ and $$0.5\,mA$$
B
$$20\,V$$ and $$2.0\,mA$$
C
$$10\,V$$ and $$0.5\,mA$$
D
Zero and therefore no current
Answer :
Zero and therefore no current
86.
Figure shows a source of alternating voltage connected to a capacitor and resistor. Which of the following phasor diagrams correctly secrobes the phase relationship between $${I_c},$$ the current between the source and the capacitor, and $${I_R},$$ the current in the resistor?

A


B


C


D


Answer :


87. Resonance frequency of a circuit is $$f.$$ If the capacitance is made 4 times the initial value, then the resonance frequency will become :
A
$$\frac{f}{2}$$
B
$$2f$$
C
$$f$$
D
$$\frac{f}{4}$$
Answer :
$$\frac{f}{2}$$
88. An $$AC$$ voltage source of variable angular frequency $$\omega $$ and fixed amplitude $${V_0}$$ is connected in series with a capacitance $$C$$ and an electric bulb of resistance $$R$$ (inductance zero). When $$\omega $$ is increase
A
the bulb glows dimmer
B
the bulb glows brighter
C
total impedance of the circuit is unchanged
D
total impedance of the circuit increases
Answer :
the bulb glows brighter
89.
Time constant of $$L-R$$ circuit will be

A
$$\frac{L}{R}$$
B
$$\frac{2L}{R}$$
C
$$\frac{L}{2R}$$
D
None of these
Answer :
$$\frac{L}{2R}$$
90.
If a direct current of value ampere is superimposed on an alternative current $$I = b\sin \omega t$$ flowing through a wire, what is the effective value of the resulting current in the circuit?
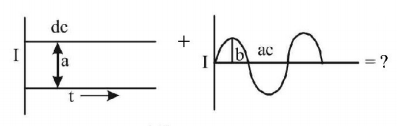
A
$${\left[ {{a^2} - \frac{1}{2}{b^2}} \right]^{\frac{1}{2}}}$$
B
$${\left[ {{a^2} + {b^2}} \right]^{\frac{1}{2}}}$$
C
$${\left[ {\frac{{{a^2}}}{2} + {b^2}} \right]^{\frac{1}{2}}}$$
D
$${\left[ {{a^2} + \frac{{{b^2}}}{2}} \right]^{\frac{1}{2}}}$$
Answer :
$${\left[ {{a^2} + \frac{{{b^2}}}{2}} \right]^{\frac{1}{2}}}$$
