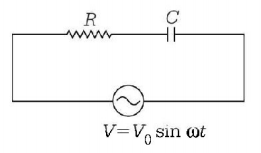
21. A series $$LR$$ circuit is connected to an $$ac$$ source of frequency $$\omega $$ and the inductive reactance is equal to $$2R.$$ A capacitance of capacitive reactance equal to $$R$$ is added in series with $$L$$ and $$R.$$ The ratio of the new power factor to the old one is
A
$$\sqrt {\frac{2}{3}} $$
B
$$\sqrt {\frac{2}{5}} $$
C
$$\sqrt {\frac{3}{2}} $$
D
$$\sqrt {\frac{5}{2}} $$
Answer :
$$\sqrt {\frac{5}{2}} $$
22.
In the given circuit, the reading of voltmeter $${V_1}$$ and $${V_2}$$ are $$300\,V$$ each. The reading to the voltmeter $${V_3}$$ and ammeter $$A$$ are respectively

A
$$150\,V,2.2\,A$$
B
$$220\,V,2.2\,A$$
C
$$220\,V,2.0\,A$$
D
$$100\,V,2.0\,A$$
Answer :
$$220\,V,2.2\,A$$
23. Power dissipated in an $$L-C-R$$ series circuit connected to an $$AC$$ source of emf $$\varepsilon $$ is
A
$$\frac{{{\varepsilon ^2}R}}{{\left[ {{R^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} \right]}}$$
B
$$\frac{{{\varepsilon ^2}\sqrt {{R^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} }}{R}$$
C
$$\frac{{{\varepsilon ^2}\left[ {{R^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} \right]}}{R}$$
D
$$\frac{{{\varepsilon ^2}R}}{{\sqrt {{R^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} }}$$
Answer :
$$\frac{{{\varepsilon ^2}R}}{{\left[ {{R^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} \right]}}$$
24.
In the $$LC$$ circuit, the current is in the direction shown and the charges on the capacitor plates have the signs shown. At this time

A
$$I$$ is increasing and $$Q$$ is increasing
B
$$I$$ is increasing and $$Q$$ is decreasing
C
$$I$$ is decreasing and $$Q$$ is increasing
D
$$I$$ is decreasing and $$Q$$ is decreasing
Answer :
$$I$$ is increasing and $$Q$$ is decreasing
25.
A series $$R-C$$ circuit is connected to an alternating voltage source. Consider two situations :
1. When capacitor is air filled.
2. When capacitor is mica filled.
Current through resistor is $$i$$ and voltage across capacitor is $$V$$ then
A
$${V_a} < {V_b}$$
B
$${V_a} > {V_b}$$
C
$${i_a} > {i_b}$$
D
$${V_a} = {V_b}$$
Answer :
$${V_a} > {V_b}$$
26. When the $$rms$$ voltages $${V_L},{V_C}$$ and $${V_R}$$ are measured respectively across the inductor $$L,$$ the capacitor $$C$$ and the resistor $$R$$ in a series $$LCR$$ circuit connected to an $$AC$$ source, it is found that the ratio $${V_L}:{V_C}:{V_R} = 1:2:3.$$ If the $$rms$$ voltage of the $$AC$$ sources is $$100\,V,$$ the $${V_R}$$ is close to :
A
$$50\,V$$
B
$$70\,V$$
C
$$90\,V$$
D
$$100\,V$$
Answer :
$$90\,V$$
27. An arc lamp requires a direct current of $$10 A$$ at $$80 V$$ to function. If it is connected to a $$220V\left( {rms} \right),50Hz\,AC$$ supply, the series inductor needed for it to work is close to :
A
$$0.044 H$$
B
$$0.065 H$$
C
$$80 H$$
D
$$0.08 H$$
Answer :
$$0.065 H$$
28.
In a circuit inductance $$L$$ and capacitance $$C$$ are connected as shown in figure. $${A_1}$$ and $${A_2}$$ are ammeters. When key $$K$$ is pressed to complete the circuit, then just after closing key $$\left( K \right),$$ the reading of current will be

A
Zero in both $${A_1}$$ and $${A_2}$$
B
maximum in both $${A_1}$$ and $${A_2}$$
C
zero in $${A_1}$$ and maximum in $${A_2}$$
D
maximum in $${A_1}$$ and zero in $${A_2}$$
Answer :
maximum in $${A_1}$$ and zero in $${A_2}$$
29. In a $$LCR$$ circuit capacitance is changed from $$C$$ to $$2C.$$ For the resonant frequency to remain unchanged, the inductance should be change from $$L$$ to
A
$$4L$$
B
$$2L$$
C
$$\frac{L}{2}$$
D
$$\frac{L}{4}$$
Answer :
$$\frac{L}{2}$$
30.
In an $$LCR$$ circuit as shown below both switches are open initially. Now switch $${S_1}$$ is closed, $${S_2}$$ kept open. ($$q$$ is charge on the capacitor and $$\tau = RC$$ is Capacitive time constant). Which of the following statements is correct ?
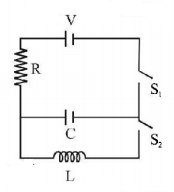
A
At, $$t = 0,q = CV\left( {1 - e} \right)$$
B
At, $$t = \tau ,q = \frac{{CV}}{2}$$
C
At, $$t = 2\tau ,q = CV\left( {1 - {e^{ - 2}}} \right)$$
D
At, $$t = 2\tau ,q = CV\left( {1 - {e^{ - 1}}} \right)$$
Answer :
At, $$t = 2\tau ,q = CV\left( {1 - {e^{ - 2}}} \right)$$