31. Which one of the following curves represents the variation of impedance $$\left( Z \right)$$ with frequency $$f$$ in series $$LCR$$ circuit?
A


B


C
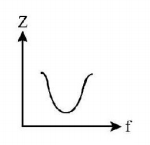

D


Answer :


32. An $$ac$$ source of angular frequency $$\omega $$ is fed across a resistor $$R$$ and a capacitor $$C$$ in series. The current registered is $$I.$$ If now the frequency of source is changed to $$\frac{\omega }{3}$$ (but maintaining the same voltage), the current in the circuit is found to be halved. Then the ratio of reactance to resistance at the original frequency $$\omega $$ is
A
$$\sqrt {\frac{3}{5}} $$
B
$$\sqrt {\frac{5}{3}} $$
C
$$\sqrt {\frac{2}{3}} $$
D
$$\sqrt {\frac{3}{2}} $$
Answer :
$$\sqrt {\frac{3}{5}} $$
33. A capacitor of $$10\,\mu F$$ and an inductor of $$1\,H$$ are joined in series. An $$ac$$ of $$50\,Hz$$ is applied to this combination. What is the impedance of the combination?
A
$$\frac{{5\left( {{\pi ^2} - 5} \right)}}{\pi }\Omega $$
B
$$\frac{{{{10}^2}\left( {10 - {\pi ^2}} \right)}}{\pi }\Omega $$
C
$$\frac{{10\left( {{\pi ^2} - 5} \right)}}{\pi }\Omega $$
D
$$\frac{{{5^2}\left( {10 - {\pi ^2}} \right)}}{\pi }\Omega $$
Answer :
$$\frac{{{{10}^2}\left( {10 - {\pi ^2}} \right)}}{\pi }\Omega $$
34.
For the circuit as shown in figure; the applied current in $$A.C.$$ circuit is zero ampere and $${I_C} = 10\,A.$$ Then the magnitude of current $${I_L}$$ is
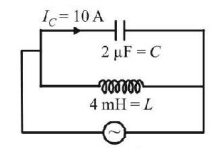
A
$$4\,A$$
B
$$10\,A$$
C
$$5\,A$$
D
undefined
Answer :
$$10\,A$$
35. The power factor in a circuit connected to an $$A.C.$$ The value of power factor is
A
unity when the circuit contains an ideal inductance only
B
unity when the circuit contains an ideal resistance only
C
zero when the circuit contains an ideal resistance only
D
unity when the circuit contains an ideal capacitance only
Answer :
unity when the circuit contains an ideal resistance only
36.
An inductor $$\left( {L = 0.03\,H} \right)$$ and a resistor $$\left( {R = 0.15\,k\Omega } \right)$$ are connected in series to a battery of $$15V$$ emf in a circuit shown below. The key $${K_1}$$ has been kept closed for a long time, Then at $$t = 0,$$ $${K_1}$$ is opened and key $${K_2}$$ is closed simultaneously. At $$t = 1\,ms,$$ the current in the circuit will be :
$$\left( {{e^5} \cong 150} \right)$$
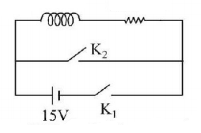
A
$$6.7\,mA$$
B
$$0.67\,mA$$
C
$$100\,mA$$
D
$$67\,mA$$
Answer :
$$0.67\,mA$$
37. For a series $$LCR$$ circuit, the power loss at resonance is
A
$$\frac{{{V^2}}}{{\omega L - \frac{1}{{\omega C}}}}$$
B
$${i^2}C\omega $$
C
$${i^2}R$$
D
$$\frac{{{V^2}}}{{\omega C}}$$
Answer :
$${i^2}R$$
38. The phase difference between the alternating current and emf is $$\frac{\pi }{2}.$$ Which of the following cannot be the constituent of the circuit?
A
$$R,L$$
B
$$C$$ alone
C
$$L$$ alone
D
$$L,C$$
Answer :
$$R,L$$
39. A capacitor in an $$LC$$ oscillator has a maximum potential difference of $$17\,V$$ and a maximum energy of $$160\,\mu J.$$ When the capacitor has a potential difference of $$5V$$ and an energy of $$10\,\mu J,$$ what is the energy stored in the magnetic field ?
A
$$10\,\mu J$$
B
$$150\,\mu J$$
C
$$160\,\mu J$$
D
$$170\,\mu J$$
Answer :
$$150\,\mu J$$
40. A coil of 40 henry inductance is connected in series with a resistance of 8 ohm and the combination is joined to the terminals of a 2 volt battery. The time constant of the circuit is
A
$$20$$ seconds
B
$$5$$ seconds
C
$$\frac{1}{5}\,\,{\text{seconds}}$$
D
$$40$$ seconds
Answer :
$$5$$ seconds