121. In an $$a.c.$$ circuit the voltage applied is $$E = {E_0}\sin \omega t.$$ The resulting current in the circuit is $$I = {I_0}\sin \left( {\omega t - \frac{\pi }{2}} \right).$$ The power consumption in the circuit is given by
A
$$P = \sqrt 2 {E_0}{I_0}$$
B
$$P = \frac{{{E_0}{I_0}}}{{\sqrt 2 }}$$
C
$$P = {\text{zero}}$$
D
$$P = \frac{{{E_0}{I_0}}}{2}$$
Answer :
$$P = {\text{zero}}$$
122.
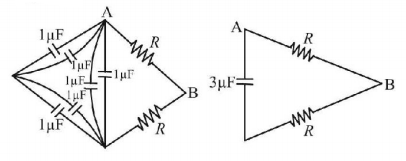
In given $$RC$$ circuit, capacitance of capacitor $${C_1} = 3\mu F$$ and $${C_2} = 1\mu F.$$ It is given that time constant of circuit between $$A$$ and $$B$$ is 3 millisecond. Value of $$R$$ will be
A
$$1\Omega $$
B
$$10\Omega $$
C
$$100\Omega $$
D
$$1000\Omega $$
Answer :
$$1000\Omega $$
123. The primary winding of transformer has 500 turns whereas its secondary has 5000 turns. The primary is connected to an $$AC$$ supply of $$20\,V-50\,Hz.$$ The secondary will have an output of
A
$$2\,V,5\,Hz$$
B
$$200\,V,500\,Hz$$
C
$$2\,V,50\,Hz$$
D
$$200\,V,50\,Hz$$
Answer :
$$200\,V,50\,Hz$$
124. The current in an $$L-R$$ circuit builds up to $${\left( {\frac{3}{4}} \right)^{th}}$$ of its steady state value in 4 seconds. The time constant of this circuit is
A
$$\frac{1}{{\ln \,2}}\sec $$
B
$$\frac{2}{{\ln \,2}}\sec $$
C
$$\frac{3}{{\ln \,2}}\sec $$
D
$$\frac{4}{{\ln \,2}}\sec $$
Answer :
$$\frac{2}{{\ln \,2}}\sec $$
125. A coil of self-inductance $$L$$ is connected in series with a bulb $$B$$ and an $$AC$$ source. Brightness of the bulb decreases when
A
frequency of the $$AC$$ source is decreased
B
number of turns in the coil is reduced
C
a capacitance of reactance $${X_C} = {X_L}$$ is included in the same circuit
D
an iron rod is inserted in the coil
Answer :
an iron rod is inserted in the coil