111. A transistor-oscillator using a resonant circuit with an inductor $$L$$ (of negligible resistance) and a capacitor $$C$$ in series produce oscillations of frequency $$f.$$ If $$L$$ is doubled and $$C$$ is changed to $$4C,$$ the frequency will be
A
$$8f$$
B
$$\frac{f}{{2\sqrt 2 }}$$
C
$$\frac{f}{2}$$
D
$$\frac{f}{4}$$
Answer :
$$\frac{f}{{2\sqrt 2 }}$$
112.
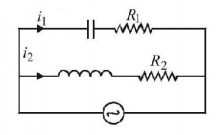
What is the amount of power delivered by the $$ac$$ source in the circuit shown (in watts).
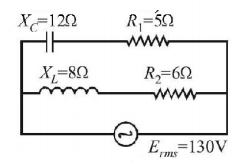
A
500 watt
B
1014 watt
C
1514 watt
D
2013 watt
Answer :
1514 watt
113.
Determine the $$rms$$ value of a semi - circular current wave which has a maximum value of $$a.$$
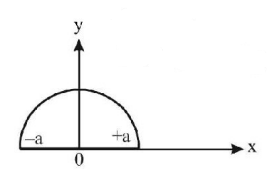
A
$$\left( {1\sqrt 2 } \right)a$$
B
$$\left( {\sqrt {\frac{3}{2}} } \right)a$$
C
$$\left( {\sqrt {\frac{2}{3}} } \right)a$$
D
$$\left( {\sqrt {\frac{1}{3}} } \right)a$$
Answer :
$$\left( {\sqrt {\frac{2}{3}} } \right)a$$
114.
Figure shows three oscillating $$LC$$ circuit with identical inductors and capacitors. If $${t_1},{t_2},{t_3}$$ are the time taken by the circuits $$I, II, III$$ for fully discharge, then
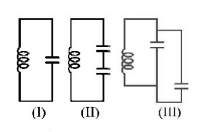
A
$${t_1} > {t_2} > {t_3}$$
B
$${t_1} < {t_2} < {t_3}$$
C
$${t_2} < {t_1} < {t_3}$$
D
$${t_3} = \sqrt {{t_1}{t_2}} $$
Answer :
$${t_2} < {t_1} < {t_3}$$
115. The primary and secondary coil of a transformer have $$50$$ and $$1500$$ turns respectively. If the magnetic flux $$\phi $$ linked with the primary coil is given by $$\phi = {\phi _0} + 4t,$$ where $$\phi $$ is in webers, $$t$$ is time in seconds and $${\phi _0}$$ is a constant, the output voltage across the secondary coil is
A
120 volts
B
220 volts
C
30 volts
D
90 volts
Answer :
120 volts
116. A resistance $$'R'$$ draws power $$'P'$$ when connected to an $$AC$$ source. If an inductance is now placed in series with the resistance, such that the impedance of the circuit becomes $$'Z'$$ the power drawn will be
A
$$P{\left( {\frac{R}{Z}} \right)^2}$$
B
$$P\sqrt {\frac{R}{Z}} $$
C
$$P\left( {\frac{R}{Z}} \right)$$
D
$$P$$
Answer :
$$P{\left( {\frac{R}{Z}} \right)^2}$$
117.
In the circuit shown below, the key $$K$$ is closed at $$t = 0.$$ The current through the battery is
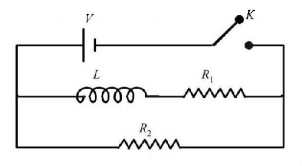
A
$$\frac{{V{R_1}{R_2}}}{{\sqrt {R_1^2 + R_2^2} }}\,\,{\text{at}}\,\,t = 0\,\,{\text{and}}\,\,\frac{V}{{{R^2}}}\,\,{\text{at}}\,\,t = \infty $$
B
$$\frac{V}{{{R^2}}}\,\,{\text{at}}\,\,t = 0\,\,{\text{and}}\,\,\frac{{V\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2}}}\,\,{\text{at}}\,\,t = \infty $$
C
$$\frac{V}{{{R^2}}}\,\,{\text{at}}\,\,t = 0\,\,{\text{and}}\,\,\frac{{V{R_1}{R_2}}}{{\sqrt {R_1^2 + R_2^2} }}\,\,{\text{at}}\,\,t = \infty $$
D
$$\frac{{V\left( {{R_1} + {R_2}} \right)}}{{{R_1}{R_2}}}\,\,{\text{at}}\,\,t = 0\,\,{\text{and}}\,\,\frac{V}{{{R^2}}}\,\,{\text{at}}\,\,t = \infty $$
Answer :
$$\frac{V}{{{R^2}}}\,\,{\text{at}}\,\,t = 0\,\,{\text{and}}\,\,\frac{{V{R_1}{R_2}}}{{\sqrt {R_1^2 + R_2^2} }}\,\,{\text{at}}\,\,t = \infty $$
118.
In an $$AC$$ circuit the emf $$\left( V \right)$$ and the current $$\left( i \right)$$ at any instant are given respectively by
$$V = {V_0}\sin \omega t,i = {i_0}\sin \left( {\omega t - \phi } \right)$$
The average power in the circuit over one cycle of $$AC$$ is
A
$$\frac{{{V_0}{i_0}}}{2}$$
B
$$\frac{{{V_0}{i_0}}}{2}\sin \phi $$
C
$$\frac{{{V_0}{i_0}}}{2}\cos \phi $$
D
$${V_0}{i_0}$$
Answer :
$$\frac{{{V_0}{i_0}}}{2}\cos \phi $$
119. An $$LCR$$ series circuit is connected to a source of alternating current. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of
A
$$\pi $$
B
$$\frac{\pi }{2}$$
C
$$\frac{\pi }{4}$$
D
zero
Answer :
zero
120. A $$100\,\Omega $$ resistance and a capacitor of $$100\,\Omega $$ reactance are connected in series across a $$220\,V$$ source. When the capacitor is $$50\% $$ charged, the peak value of the displacement current is
A
$$2.2\,A$$
B
$$11\,A$$
C
$$4.4\,A$$
D
$$11\sqrt 2 A$$
Answer :
$$2.2\,A$$