91.
Figure shows an iron - cored transformer assumed to be $$100\% $$ efficient. The ratio of the secondary turns to the primary turns is $$1 : 20.$$
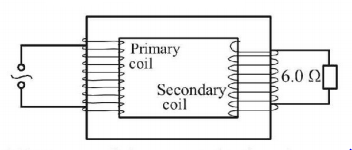
A $$240\,V$$ $$ac$$ supply is connected to the primary coil and a $$6\,W$$ resistor is corrected to the secondary coil. What is the current in the primary coil?
A
$$0.10\,A$$
B
$$0.14\,A$$
C
$$2\,A$$
D
$$40\,A$$
Answer :
$$0.10\,A$$
92.
The two capacitors, shown in the circuit, are initially uncharged and the cell is ideal. The switch $$S$$ is closed at $$t = 0.$$ Which of the following functions represents the current $$i\left( t \right),$$ through the cell as a function of time? Here $${i_0},{i_1},{i_2}$$ are constants.
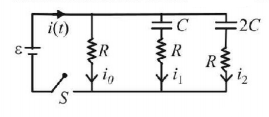
A
$$i\left( t \right) = {i_0} + {i_1}{e^{\frac{{ - t}}{\tau }}};\tau = 3C \times \frac{R}{3}$$
B
$$i\left( t \right) = {i_0} + {i_1}{e^{\frac{{ - t}}{\tau }}} + {i_2}{e^{\frac{{ - t}}{{2\tau }}}};\tau = RC$$
C
$$i\left( t \right) = {i_1} + {i_1}{e^{\frac{{ - t}}{\tau }}};\tau = 3C \times \frac{R}{3}$$
D
$$i\left( t \right) = {i_0} + {i_1}{e^{\frac{{ - t}}{\tau }}};\tau = 3RC$$
Answer :
$$i\left( t \right) = {i_0} + {i_1}{e^{\frac{{ - t}}{\tau }}} + {i_2}{e^{\frac{{ - t}}{{2\tau }}}};\tau = RC$$
93. A $$220\,V$$ input is supplied to a transformer. The output circuit draws a current of $$2.0\,A$$ at $$440\,V.$$ If the efficiency of the transformer is $$80\% ,$$ the current drawn by the primary windings of the transformer is
A
$$3.6\,A$$
B
$$2.8\,A$$
C
$$2.5\,A$$
D
$$5.0\,A$$
Answer :
$$5.0\,A$$
94.
The current $$\left( I \right)$$ in the inductance is varying with time according to the plot shown in figure.
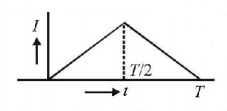
Which one of the following is the correct variation of voltage with time in the coil?
A
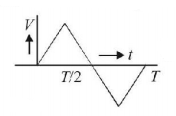

B
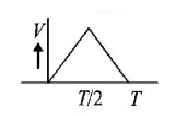

C


D


Answer :


95. In an electrical circuit, $$R,L,C$$ and an $$AC$$ voltage source are all connected in series. When $$L$$ is removed from the circuit, the phase difference between the voltage and the current in the circuit is $$\frac{\pi }{3}.$$ If instead, $$C$$ is removed from the circuit, the phase difference is again $$\frac{\pi }{3}.$$ The power factor of the circuit is
A
$$\frac{1}{2}$$
B
$$\frac{1}{{\sqrt 2 }}$$
C
$$1$$
D
$$\frac{{\sqrt 3 }}{2}$$
Answer :
$$1$$
96. A transformer is used to light a $$140\,W,24\,V$$ bulb from a $$240\,V$$ $$a.c.$$ mains. The current in the main cable is $$0.7\,A.$$ The efficiency of the transformer is
A
$$63.8\% $$
B
$$83.3\% $$
C
$$16.7\% $$
D
$$36.2\% $$
Answer :
$$83.3\% $$
97. A step up transformer operates on a $$230\,V$$ line and supplies a current of 2 ampere. The ratio of primary and secondary winding is $$1:25.$$ The current in primary
A
$$25\,A$$
B
$$50\,A$$
C
$$15\,A$$
D
$$12.5\,A$$
Answer :
$$50\,A$$
98. The time constant of $$C-R$$ circuit is
A
$$\frac{1}{{CR}}$$
B
$$\frac{C}{R}$$
C
$$CR$$
D
$$\frac{R}{C}$$
Answer :
$$CR$$
99. A transformer having efficiency of $$90\% $$ is working on $$200\,V$$ and $$3\,kW$$ power supply. If the current in the secondary coil is $$6\,A,$$ the voltage across the secondary coil and the current in the primary coil respectively are
A
$$300\,V,15\,A$$
B
$$450\,V,15\,A$$
C
$$450\,V,13.5\,A$$
D
$$600\,V,15\,A$$
Answer :
$$450\,V,15\,A$$
100. For an $$RLC$$ circuit driven with voltage of amplitude $${v_m}$$ and frequency $${\omega _0} = \frac{1}{{\sqrt {LC} }}$$ the current exhibits resonance. The quality factor, $$Q$$ is given by:
A
$$\frac{{{\omega _0}L}}{R}$$
B
$$\frac{{{\omega _0}R}}{L}$$
C
$$\frac{R}{{\left( {{\omega _0}C} \right)}}$$
D
$$\frac{{CR}}{{{\omega _0}}}$$
Answer :
$$\frac{{{\omega _0}L}}{R}$$