81.
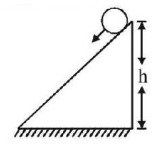
A solid cylinder of mass $$m$$ & radius $$R$$ rolls down inclined plane without slipping. The speed of its $$C.M.$$ when it reaches the bottom is
A
$$\sqrt {2gh} $$
B
$$\sqrt {\frac{{4gh}}{3}} $$
C
$$\sqrt {\frac{3}{{4gh}}} $$
D
$$\sqrt {4gh} $$
Answer :
$$\sqrt {\frac{{4gh}}{3}} $$
82. The angular speed of an engine wheel making $$90\,rev/min$$ is
A
$$1.5\,\pi \,rad/s$$
B
$$3\,\pi \,rad/s$$
C
$$4.5\,\pi \,rad/s$$
D
$$6\,\pi \,rad/s$$
Answer :
$$3\,\pi \,rad/s$$
83. A horizontal circular plate is rotating about a vertical axis passing through its centre with an angular velocity $${\omega _0}.$$ A man sitting at the centre having two blocks in his hands stretches out his hands so that the moment of inertia of the system doubles. If the kinetic energy of the system is $$K$$ initially, its final kinetic energy will be-
A
$$2\,K$$
B
$$\frac{K}{2}$$
C
$$K$$
D
$$\frac{K}{4}$$
Answer :
$$\frac{K}{2}$$
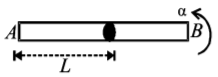
84.
A long horizontal rod has a bead which can slide along its length and initially placed at a distance $$L$$ from one end $$A$$ of the rod. The rod is set in angular motion about $$A$$ with constant angular acceleration $$\alpha .$$ If the coefficient of friction between the rod and the bead is $$\mu ,$$ and gravity is neglected, then the time after which the bead starts slipping is
A
$$\sqrt {\frac{\mu }{\alpha }} $$
B
$$\frac{\mu }{{\sqrt \alpha }}$$
C
$$\frac{1}{{\sqrt {\mu \alpha } }}$$
D
infinitesimal
Answer :
$$\sqrt {\frac{\mu }{\alpha }} $$
85. A pulley of radius $$2 \,m$$ is rotated about its axis by a force $$F = \left( {20t - 5{t^2}} \right)$$ newton (where $$t$$ is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is $$10\,kg - {m^2}$$ the number of rotations made by the pulley before its direction of motion is reversed, is:
A
more than $$3$$ but less than $$6$$
B
more than $$6$$ but less than $$9$$
C
more than $$9$$
D
less than $$3$$
Answer :
more than $$3$$ but less than $$6$$
86. A wheel having moment of inertia $$2\,kg - {m^2}$$ about its vertical axis, rotates at the rate of $$60\,rpm$$ about this axis, The torque which can stop the wheel’s rotation in one minute would be
A
$$1.12\,Nm$$
B
$$0.83\,Nm$$
C
$$0.55\,Nm$$
D
$$0.21\,Nm$$
Answer :
$$0.21\,Nm$$
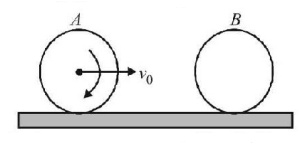
87.
A hollow smooth uniform sphere $$A$$ of mass $$m$$ rolls without sliding on a smooth horizontal surface. It collides head on elastically with another stationary smooth solid sphere $$B$$ of the same mass m and same radius. The ratio of kinetic energy of $$B$$ to that of $$A$$ just after the collision is
A
$$1:1$$
B
$$2:3$$
C
$$3:2$$
D
None of these
Answer :
$$3:2$$
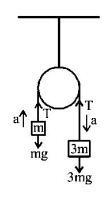
88. A pulley fixed to the ceiling carries a string with blocks of mass $$m$$ and $$3\,m$$ attached to its ends. The masses of string and pulley are negligible. When the system is released, its centre of mass moves with what acceleration ?
A
$$0$$
B
$$ - \frac{g}{4}$$
C
$$\frac{g}{2}$$
D
$$ - \frac{g}{2}$$
Answer :
$$\frac{g}{2}$$
89. Three identical spheres, each of mass $$1\,kg$$ are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked $$P,Q,R$$ respectively, the distance of centre of mass of the system from $$P$$ is
A
$$\frac{{PQ + PR + QR}}{3}$$
B
$$\frac{{PQ + PR}}{3}$$
C
$$\frac{{PQ + QR}}{3}$$
D
$$\frac{{PR + QR}}{3}$$
Answer :
$$\frac{{PQ + PR}}{3}$$
90.
A roller is made by joining together two cones at their vertices $$O.$$ It is kept on two rails $$AB$$ and $$CD,$$ which are placed asymmetrically (see figure), with its axis perpendicular to $$CD$$ and its centre $$O$$ at the centre of line joining $$AB$$ and $$CD$$ (see figure). It is given a light push so that it starts rolling with its centre $$O$$ moving parallel to $$CD$$ in the direction shown. As it moves, the roller will tend to:

A
go straight.
B
turn left and right alternately.
C
turn left.
D
turn right.
Answer :
turn left.