31. A solid sphere, a hollow sphere and a ring are released from top of an inclined plane (frictionless) so that they slide down the plane. Then maximum acceleration down the plane is for (no rolling)-
A
Solid sphere
B
Hollow sphere
C
Ring
D
All same
Answer :
All same
32. A particle performing uniform circular motion has angular frequency is doubled & its kinetic energy halved, then the new angular momentum is-
A
$$\frac{L}{4}$$
B
$$2L$$
C
$$4L$$
D
$$\frac{L}{2}$$
Answer :
$$\frac{L}{4}$$
33.
A slender uniform rod of mass $$M$$ and length $$\ell $$ is pivoted at one end so that it can rotate in a vertical plane (see figure). There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle $$\theta $$ with the vertical is

A
$$\frac{{3g}}{{2\ell }}\cos \theta $$
B
$$\frac{{2g}}{{3\ell }}\cos \theta $$
C
$$\frac{{3g}}{{2\ell }}\sin \theta $$
D
$$\frac{{2g}}{{2\ell }}\sin \theta $$
Answer :
$$\frac{{3g}}{{2\ell }}\sin \theta $$
34. Two objects $$P$$ and $$Q$$ initially at rest move towards each other under mutual force of attraction. At the instant when the velocity of $$P$$ is $$v$$ and that of $$Q$$ is $$2v,$$ the velocity of centre of mass of the system is
A
$$v$$
B
$$3v$$
C
$$2v$$
D
zero
Answer :
zero
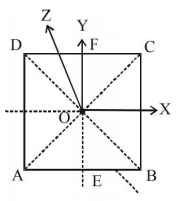
35.
For the given uniform square lamina $$ABCD,$$ whose centre is $$o,$$

A
$${I_{AC}} = \sqrt 2 {I_{EF}}$$
B
$$\sqrt 2 {I_{AC}} = {I_{EF}}$$
C
$${I_{AD}} = 3{I_{EF}}$$
D
$${I_{AC}} = {I_{EF}}$$
Answer :
$${I_{AC}} = {I_{EF}}$$
36. The moment of inertia of a body about a given axis is $$1.2\,kg - {m^2}.$$ Initially, the body is at rest. In order to produce a rotational kinetic energy of $$1500\,J,$$ an angular acceleration of $$25\,rad/{s^2}$$ must be applied about that axis for a duration of
A
$$4\,s$$
B
$$2\,s$$
C
$$8\,s$$
D
$$10\,s$$
Answer :
$$2\,s$$
37.
An equilateral triangle $$ABC$$ formed from a uniform wire has two small identical beads initially located at $$A.$$ The triangle is set rotating about the vertical axis $$AO.$$ Then the beads are released from rest simultaneously and allowed to slide down, one along $$AB$$ and the other along $$AC$$ as shown. Neglecting frictional effects, the quantities that are conserved as the beads slide down, are

A
angular velocity and total energy (kinetic and potential)
B
total angular momentum and total energy
C
angular velocity and moment of inertia about the axis of rotation
D
total angular momentum and moment of inertia about the axis of rotation
Answer :
total angular momentum and total energy
38.
A wheel of radius $$0.1\,m$$ (wheel $$A$$) is attached by a non-stretching belt to a wheel of radius $$0.2\,m$$ (wheel $$B$$ ). The belt does not slip. By the time wheel $$B$$ turns through $$1$$ revolution, wheel $$A$$ will rotate through

A
$$\frac{1}{2}$$ revolution
B
$$1$$ revolution
C
$$2$$ revolution
D
$$4$$ revolution
Answer :
$$2$$ revolution
39.
The following bodies are made to roll up (without slipping) the same inclined plane from a horizontal plane:
(i) a ring of radius $$R,$$ (ii) a solid cylinder of radius $$\frac{R}{2}$$ and (iii) a solid sphere of radius $$\frac{R}{4}$$
If, in each case, the speed of the center of mass at the bottom of the incline is same, the ratio of the maximum heights they climb is:
A
$$4:3:2$$
B
$$10:15:7$$
C
$$14:15:20$$
D
$$2:3:4$$
Answer :
$$14:15:20$$
40. Two particles which are initially at rest, move towards each other under the action of their internal attraction. If their speeds are $$v$$ and $$2v$$ at any instant, then the speed of centre of mass of the system will be:
A
$$2v$$
B
zero
C
$$1.5$$
D
$$v$$
Answer :
zero