91. A solid sphere of radius $$R$$ is placed on a smooth horizontal surface. A horizontal force $$F$$ is applied at height $$h$$ from the lowest point. For the maximum acceleration of the centre of mass
A
$$h = R$$
B
$$h = 2R$$
C
$$h = 0$$
D
the acceleration will be same whatever $$h$$ may be
Answer :
the acceleration will be same whatever $$h$$ may be
92.
A block of mass $$m$$ is at rest under the action of force $$F$$ against a wall as shown in figure. Which of the following statement is incorrect?

A
$$f = mg\left[ {f{\text{ friction force}}} \right]$$
B
$$F = N\left[ {{ N \,\text{normal force}}} \right]$$
C
$$F$$ will not produce torque
D
$$N$$ will not produce torque
Answer :
$$N$$ will not produce torque
93. Distance of the centre of mass of a solid uniform cone from its vertex is $${z_0}.$$ If the radius of its base is $$R$$ and its height is $$h$$ then $${z_0}$$ is equal to:
A
$$\frac{{5h}}{8}$$
B
$$\frac{{3{h^2}}}{{8R}}$$
C
$$\frac{{{h^2}}}{{4R}}$$
D
$$\frac{{3h}}{4}$$
Answer :
$$\frac{{3h}}{4}$$
94.
A $$'T \,’$$ shaped object with dimensions shown in the figure, is lying on a smooth floor. A force $$'\vec F \,'$$ is applied at the point $$P$$ parallel to $$AB,$$ such that the object has only the translational motion without rotation. Find the location of $$P$$ with respect to $$C.$$

A
$$\frac{3}{2}\ell $$
B
$$\frac{2}{3}\ell $$
C
$$\ell $$
D
$$\frac{4}{3}\ell $$
Answer :
$$\frac{4}{3}\ell $$
95. A bob of mass $$m$$ attached to an inextensible string of length $$l$$ is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed $$\omega \,rad/s$$ about the vertical. About the point of suspension:
A
angular momentum is conserved.
B
angular momentum changes in magnitude but not in direction.
C
angular momentum changes in direction but not in magnitude.
D
angular momentum changes both in direction and magnitude.
Answer :
angular momentum changes in direction but not in magnitude.
96. If the angular momentum of a particle of mass $$m$$ rotating along a circular path of radius $$r$$ with uniform speed is $$L,$$ the centripetal force acting on the particle is
A
$$\frac{{{L^2}}}{{m{r^2}}}$$
B
$$\frac{{{L^2}}}{{mr}}$$
C
$$\frac{L}{{mr}}$$
D
$$\frac{{{L^2}m}}{r}$$
Answer :
$$\frac{{{L^2}}}{{mr}}$$
97. A round disc of moment of inertia $${I_2}$$ about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia $${I_1}$$ rotating with an angular velocity $$\omega $$ about the same axis. The final angular velocity of the combination of discs is
A
$$\frac{{{I_2}\omega }}{{{I_1} + {I_2}}}$$
B
$$\omega $$
C
$$\frac{{{I_1}\omega }}{{{I_1} + {I_2}}}$$
D
$$\frac{{\left( {{I_1} + {I_2}} \right)\omega }}{{{I_1}}}$$
Answer :
$$\frac{{{I_1}\omega }}{{{I_1} + {I_2}}}$$
98. A solid cylinder of mass $$M$$ and radius $$R$$ rolls down an inclined plane of height $$h$$ without slipping. The speed of its centre of mass when it reaches the bottom is
A
$$\sqrt {2gh} $$
B
$$\sqrt {\frac{{4gh}}{3}} $$
C
$$\sqrt {\frac{{3gh}}{4}} $$
D
$$\sqrt {\frac{{4g}}{h}} $$
Answer :
$$\sqrt {\frac{{4gh}}{3}} $$
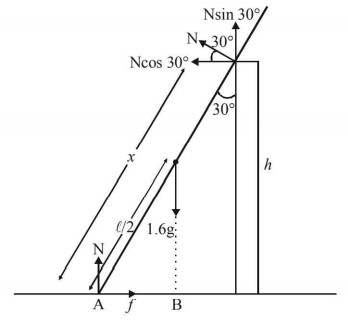
99.
A uniform wooden stick of mass $$1.6 \,kg$$ and length $$l$$ rests in an inclined manner on a smooth, vertical wall of height $$h\left( { < l} \right)$$ such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of $${30^ \circ }$$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio $$\frac{h}{l}$$ and the frictional force $$f$$ at the bottom of the stick are-
$$\left( {g = 10\,m{s^{ - 2}}} \right)$$
A
$$\frac{h}{l} = \frac{{\sqrt 3 }}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
B
$$\frac{h}{l} = \frac{3}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
C
$$\frac{h}{l} = \frac{{3\sqrt 3 }}{{16}},\,\,f = \frac{{8\sqrt 3 }}{3}N$$
D
$$\frac{h}{l} = \frac{{3\sqrt 3 }}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
Answer :
$$\frac{h}{l} = \frac{{3\sqrt 3 }}{{16}},\,\,f = \frac{{16\sqrt 3 }}{3}N$$
100.
Two particles, each of mass $$2\,kg$$ are put at $$\left( {2m,0} \right)$$ and $$\left( {0,2m} \right),$$ as shown in figure. Now $$1\,kg$$ mass of particle $$A$$ is put on to the particle $$B.$$ The change in $$x$$-coordinate of centre of mass of the system is

A
$$0.5\,m$$
B
$$1\,m$$
C
$$1.5\,m$$
D
None of these
Answer :
$$0.5\,m$$