121.
An L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If $$AB=BC,$$ and the angle made by $$AB$$ with downward vertical is $$\theta ,$$ then:

A
$$\tan \theta = \frac{1}{{2\sqrt 3 }}$$
B
$$\tan \theta = \frac{1}{2}$$
C
$$\tan \theta = \frac{2}{{\sqrt 3 }}$$
D
$$\tan \theta = \frac{1}{3}$$
Answer :
$$\tan \theta = \frac{1}{3}$$
122.
$$ABC$$ is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. $${I_{AB}},{I_{BC}}$$ and $${I_{CA}}$$ are the moments of inertia of the plate about $$AB,BC$$ and $$CA$$ as axes respectively. Which one of the following relations is correct?

A
$${I_{AB}} > {I_{BC}}$$
B
$${I_{BC}} > {I_{AC}}$$
C
$${I_{AB}} + {I_{BC}} = {I_{CA}}$$
D
$${I_{CA}}$$ is maximum
Answer :
$${I_{BC}} > {I_{AC}}$$
123. A round uniform body of radius $$R,$$ mass $$M$$ and moment of inertia $$I$$ rolls down (without slipping) an inclined plane making an angle $$\theta $$ with the horizontal. Then its acceleration is-
A
$$\frac{{g\sin \theta }}{{\frac{{1 - M{R^2}}}{I}}}$$
B
$$\frac{{g\sin \theta }}{{\frac{{1 + I}}{{M{R^2}}}}}$$
C
$$\frac{{g\sin \theta }}{{\frac{{1 + M{R^2}}}{I}}}$$
D
$$\frac{{g\sin \theta }}{{\frac{{1 - I}}{{M{R^2}}}}}$$
Answer :
$$\frac{{g\sin \theta }}{{\frac{{1 + I}}{{M{R^2}}}}}$$
124.
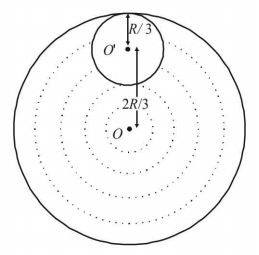
From a uniform circular disc of radius $$R$$ and mass $$9 M,$$ a small disc of radius $$\frac{R}{3}$$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing, through centre of disc is:

A
$$4M{R^2}$$
B
$$\frac{{40}}{9}M{R^2}$$
C
$$10M{R^2}$$
D
$$\frac{{37}}{9}M{R^2}$$
Answer :
$$4M{R^2}$$
125. The speed of a homogeneous solid sphere after rolling down an inclined plane of vertical height $$h$$ from rest without sliding is
A
$$\sqrt {\frac{{10}}{7}gh} $$
B
$$\sqrt {gh} $$
C
$$\sqrt {\frac{6}{5}gh} $$
D
$$\sqrt {\frac{4}{3}gh} $$
Answer :
$$\sqrt {\frac{{10}}{7}gh} $$
126.
Consider regular polygons with number of sides $$n = 3, \,4, \,5\,....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta .$$ Then $$\Delta $$ depends on $$n$$ and $$h$$ as

A
$$\Delta = h\,{\sin ^2}\left( {\frac{\pi }{n}} \right)$$
B
$$\Delta = h\left( {\frac{1}{{\cos \left( {\frac{\pi }{n}} \right)}} - 1} \right)$$
C
$$\Delta = h\sin \left( {\frac{{2\pi }}{n}} \right)$$
D
$$\Delta = h\,{\tan ^2}\left( {\frac{\pi }{n}} \right)$$
Answer :
$$\Delta = h\left( {\frac{1}{{\cos \left( {\frac{\pi }{n}} \right)}} - 1} \right)$$
127.
Two spheres $$A$$ and $$B$$ of masses $$m$$ and $$2m$$ and radii $$2R$$ and $$R$$ respectively are placed in contact as shown. The $$COM$$ of the system lies

A
inside $$A$$
B
inside $$B$$
C
at the point of contact
D
None of these
Answer :
at the point of contact
128. In a bicycle, the radius of rear wheel is twice the radius of front wheel. It $${r_f}$$ and $${r_r}$$ are the radii and $${v_f}$$ and $${v_r}$$ are the speeds of topmost points of wheels then
A
$${v_r} = 2{v_f}$$
B
$${v_f} = 2{v_r}$$
C
$${v_f} = {v_r}$$
D
$${v_f} = 4{v_r}$$
Answer :
$${v_f} = {v_r}$$
129. Two racing cars of masses $$m$$ and $$4m$$ are moving in circles of radii $$r$$ and $$2r$$ respectively. If their speeds are such that each makes a complete circle in the same time, then the ratio of the angular speeds of the first to the second car is
A
$$8:1$$
B
$$4:1$$
C
$$2:1$$
D
$$1:1$$
Answer :
$$1:1$$
130. The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is
A
$$1:\sqrt 2 $$
B
$$1:3$$
C
$$2:1$$
D
$$\sqrt 5 :\sqrt 6 $$
Answer :
$$\sqrt 5 :\sqrt 6 $$