51. A solid sphere of mass $$m$$ and radius $$R$$ is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation $$\left( {\frac{{{E_{{\text{sphere}}}}}}{{{E_{{\text{cylinder}}}}}}} \right)$$ will be
A
$$2:3$$
B
$$1:5$$
C
$$1:4$$
D
$$3:1$$
Answer :
$$1:5$$
52. A solid cylinder of mass $$50\,kg$$ and radius $$0.5\,m$$ is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of $$2$$ revolutions $${s^{ - 2}}$$ is
A
$$25\,N$$
B
$$50\,N$$
C
$$78.5\,N$$
D
$$157\,N$$
Answer :
$$157\,N$$
53. The instantaneous angular position of a point on a rotating wheel is given by the equation $$Q\left( t \right) = 2{t^3} - 6{t^2}.$$ The torque on the wheel becomes zero at
A
$$t = 0.5\,s$$
B
$$t = 0.25\,s$$
C
$$t = 2\,s$$
D
$$t = 1\,s$$
Answer :
$$t = 1\,s$$
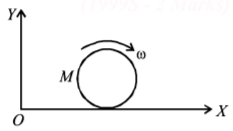
54.
A disc of mass $$M$$ and radius $$R$$ is rolling with angular speed $$\omega $$ on a horizontal plane as shown in Figure. The magnitude of angular momentum of the disc about the origin $$O$$ is
A
$$\left( {\frac{1}{2}} \right)M{R^2}\omega $$
B
$$M{R^2}\omega $$
C
$$\left( {\frac{3}{2}} \right)M{R^2}\omega $$
D
$$2M{R^2}\omega $$
Answer :
$$\left( {\frac{3}{2}} \right)M{R^2}\omega $$
55. The moment of inertia of a uniform cylinder of length $$\ell $$ and radius $$R$$ about its perpendicular bisector is $$I.$$ What is the ratio $$\frac{\ell }{R}$$ such that the moment of inertia is minimum?
A
$$1$$
B
$$\frac{3}{{\sqrt 2 }}$$
C
$$\sqrt {\frac{3}{2}} $$
D
$$\frac{{\sqrt 3 }}{2}$$
Answer :
$$\sqrt {\frac{3}{2}} $$
56. A tube of length $$L$$ is filled completely with an incompressible liquid of mass $$M$$ and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity $$\omega .$$ The force exerted by the liquid at the other end is
A
$$\frac{{ML{\omega ^2}}}{2}$$
B
$$\frac{{M{L^2}\omega }}{2}$$
C
$$ML{\omega ^2}$$
D
$$\frac{{M{L^2}{\omega ^2}}}{2}$$
Answer :
$$\frac{{ML{\omega ^2}}}{2}$$
57. Moment of inertia of a circular wire of mass $$M$$ and radius $$R$$ about its diameter is
A
$$\frac{{M{R^2}}}{2}$$
B
$$M{R^2}$$
C
$$2M{R^2}$$
D
$$\frac{{M{R^2}}}{4}$$
Answer :
$$\frac{{M{R^2}}}{2}$$
58. The minimum velocity $$\left( {{\text{in m}}{{\text{s}}^{ - 1}}} \right)$$ with which a car driver must traverse a flat curve of radius $$150 \,m$$ and coefficient of friction $$0.6$$ to avoid skidding is-
A
60
B
30
C
15
D
25
Answer :
30
59. A gramophone record is revolving with an angular velocity $$\omega .$$ A coin is placed at a distance $$r$$ from the centre of the record. The static coefficient of friction is $$\mu .$$ The coin will revolve with the record if
A
$$r = \mu g{\omega ^2}$$
B
$$r < \frac{{{\omega ^2}}}{{\mu g}}$$
C
$$r \leqslant \frac{{\mu g}}{{{\omega ^2}}}$$
D
$$r \geqslant \frac{{\mu g}}{{{\omega ^2}}}$$
Answer :
$$r \leqslant \frac{{\mu g}}{{{\omega ^2}}}$$
60. If the linear density (mass per unit length) of a rod of length $$3m$$ is proportional to $$x,$$ where $$x$$ is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is
A
$$2.5\,m$$
B
$$1\,m$$
C
$$1.5\,m$$
D
$$2\,m$$
Answer :
$$2\,m$$