131.
A uniform rod of length $$l$$ and mass $$m$$ is free to rotate in a vertical plane about $$A.$$ The rod initially in horizontal position is released. The initial angular acceleration of the rod is
(moment of inertia of rod about $$A$$ is $$\frac{{m{l^2}}}{3}$$ )

A
$$\frac{{3g}}{{2l}}$$
B
$$\frac{{2l}}{{3g}}$$
C
$$\frac{{3g}}{{2{l^2}}}$$
D
$$mg\frac{l}{2}$$
Answer :
$$\frac{{3g}}{{2l}}$$
132. The angular momentum of a body with mass $$\left( m \right)$$ moment of inertia $$\left( I \right)$$ and angular velocity $$\left( \omega \right)\,rad/s$$ is equal to
A
$$I\omega $$
B
$$I{\omega ^2}$$
C
$$\frac{I}{\omega }$$
D
$$\frac{I}{{{\omega ^2}}}$$
Answer :
$$I\omega $$
133. A particle of mass $$m = 5\,kg$$ is moving with a uniform speed $$v = 3\sqrt 2 $$ in the $$XOY$$ plane along the line $$Y = X + 4.$$ The magnitude of the angular momentum of the particle about the origin is
A
$$60\,unit$$
B
$$40\sqrt 2 \,unit$$
C
zero
D
$$7.5\,unit$$
Answer :
$$60\,unit$$
134.
$$M.I$$ of a circular loop of radius $$R$$ about the axis in figure is

A
$$M{R^2}$$
B
$$\left( {\frac{3}{4}} \right)M{R^2}$$
C
$$\frac{{M{R^2}}}{2}$$
D
$$2M{R^2}$$
Answer :
$$\left( {\frac{3}{4}} \right)M{R^2}$$
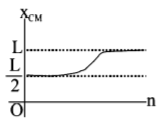
135. A thin rod of length $$'L'$$ is lying along the x-axis with its ends at $$x=0$$ and $$x=L.$$ Its linear density (mass/length) varies with $$x$$ as $$k{\left( {\frac{x}{L}} \right)^n},$$ where $$n$$ can be zero or any positive number. If the position $${x_{CM}},$$ of the centre of mass of the rod is plotted against $$'n',$$ which of the following graphs best approximates the dependence of $${x_{CM}},$$ on $$n$$ ?
A


B


C


D

Answer :


136.
A particle of mass $$m$$ moves along line $$PC$$ with velocity $$v$$ as shown. What is the angular momentum of the particle about $$P$$ ?

A
$$mvL$$
B
$$mvl$$
C
$$mvr$$
D
$$Zero$$
Answer :
$$Zero$$
137.
A small object of uniform density rolls up a curved surface with an initial velocity $$v.$$ It reaches up to a maximum height of $$\frac{{3{v^2}}}{{4g}}$$ with respect to the initial position. The object is

A
Ring
B
Solid sphere
C
Hollow sphere
D
Disc
Answer :
Disc
138.
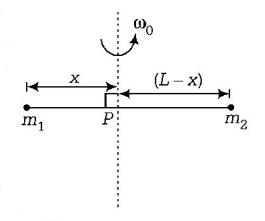
Point masses $${m_1}$$ and $${m_2}$$ are placed at the opposite ends of a rigid rod of length $$L$$ and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point $$P$$ on this rod through which the axis should pass, so that the work required to set the rod rotating with angular velocity $${\omega _0}$$ is minimum, is given by

A
$$x = \frac{{{m_1}L}}{{{m_1} + {m_2}}}$$
B
$$x = \frac{{{m_1}}}{{{m_2}}}L$$
C
$$x = \frac{{{m_2}}}{{{m_1}}}L$$
D
$$x = \frac{{{m_2}L}}{{{m_1} + {m_2}}}$$
Answer :
$$x = \frac{{{m_2}L}}{{{m_1} + {m_2}}}$$
139.
Linear acceleration of cylinder of mass $${m_2}$$ is $${a_2}.$$ Then angular acceleration $${\alpha _2}$$ is (given that there is no slipping).

A
$$\frac{{{a_2}}}{R}$$
B
$$\frac{{\left( {{a_2} + g} \right)}}{R}$$
C
$$\frac{{2\left( {{a_2} + g} \right)}}{R}$$
D
None of these
Answer :
$$\frac{{2\left( {{a_2} + g} \right)}}{R}$$
140. Four point masses, each of value $$m,$$ are placed at the corners of a square $$ABCD$$ of side $$\ell .$$ The moment of inertia of this system about an axis passing through $$A$$ and parallel to $$BD$$ is
A
$$2m{\ell ^2}$$
B
$$\sqrt 3 m{\ell ^2}$$
C
$$3m{\ell ^2}$$
D
$$m{\ell ^2}$$
Answer :
$$3m{\ell ^2}$$