201. A bullet of mass $$10\,g$$ and speed $$500\,m/s$$ is fired into a door and gets embedded exactly at the centre of the door. The door is $$1.0\,m$$ wide and weighs $$12\,kg.$$ It is hinged at one end and rotates about a vertical axis practically without friction. The angular speed of the door just after the bullet embeds into it will be :
A
$$6.25\,rad/\sec $$
B
$$0.625\,rad/\sec $$
C
$$3.35\,rad/\sec $$
D
$$0.335\,rad/\sec $$
Answer :
$$0.625\,rad/\sec $$
202.
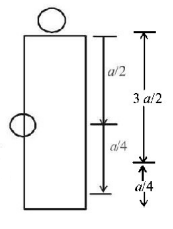
A particle of mass $$m$$ is attached to a thin uniform rod of length a and mass $$4\,m.$$ The distance of the particle from the centre of mass of the rod is $$\frac{a}{4}.$$ The moment of inertia of the combination about an axis passing through $$O$$ normal to the rod is
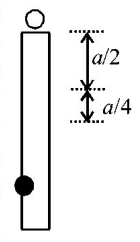
A
$$\frac{{64}}{{48}}m{a^2}$$
B
$$\frac{{91}}{{48}}m{a^2}$$
C
$$\frac{{27}}{{48}}m{a^2}$$
D
$$\frac{{51}}{{48}}m{a^2}$$
Answer :
$$\frac{{91}}{{48}}m{a^2}$$
203.
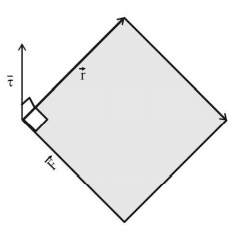
A disc is rolling without slipping with angular velocity $$\omega .$$ $$P$$ and $$Q$$ are two points equidistant from the centre $$C.$$ The order of magnitude of velocity is
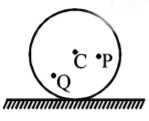
A
$${v_Q} > {v_C} > {v_P}$$
B
$${v_P} > {v_C} > {v_Q}$$
C
$${v_P} = {v_C},\,{v_Q} = \frac{{{v_C}}}{2}$$
D
$${v_P} < {v_C} > {v_Q}$$
Answer :
$${v_P} > {v_C} > {v_Q}$$
204. A ball of mass $$0.25\,kg$$ attached to the end of a string of length $$1.96\,m$$ is moving in a horizontal circle. The string will break if the tension is more than $$25\,N.$$ What is the maximum speed with which the ball can be moved ?
A
$$14\,m/s$$
B
$$3\,m/s$$
C
$$3.92\,m/s$$
D
$$5\,m/s$$
Answer :
$$14\,m/s$$
205. A thin circular ring of mass $$M$$ and radius $$r$$ is rotating about its axis with a constant angular velocity $$\omega .$$ Four objects each of mass $$m,$$ are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
A
$$\frac{{\left( {M + 4m} \right)\omega }}{M}$$
B
$$\frac{{\left( {M - 4m} \right)\omega }}{{M + 4m}}$$
C
$$\frac{{M\omega }}{{4m}}$$
D
$$\frac{{M\omega }}{{M + 4m}}$$
Answer :
$$\frac{{M\omega }}{{M + 4m}}$$
206. Angular momentum is
A
vector (axial)
B
vector (polar)
C
scalar
D
None of these
Answer :
vector (axial)
207. Let $${\vec F}$$ be the force acting on a particle having position vector $$\vec r,$$ and $${\vec T}$$ be the torque of this force about the origin. Then-
A
$$\vec r.\vec T = 0{\text{ and }}\vec F.\vec T \ne 0$$
B
$$\vec r.\vec T \ne 0{\text{ and }}\vec F.\vec T = 0$$
C
$$\vec r.\vec T \ne 0{\text{ and }}\vec F.\vec T \ne 0$$
D
$$\vec r.\vec T = 0{\text{ and }}\vec F.\vec T = 0$$
Answer :
$$\vec r.\vec T = 0{\text{ and }}\vec F.\vec T = 0$$
208.
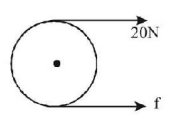
A tangential force of $$20\,N$$ is applied on a cylinder of mass $$4\,kg$$ and moment of inertia $$0.02\,kg\,{m^2}$$ about its own axis. If the cylinder rolls without slipping, then linear acceleration of its centre of mass will be
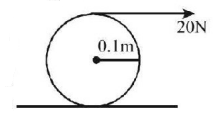
A
$$6.7\,m/{s^2}$$
B
$$10\,m/{s^2}$$
C
$$3.3\,m/{s^2}$$
D
None of these
Answer :
$$6.7\,m/{s^2}$$
209. Two bodies of masses $$2\,kg$$ and $$4\,kg$$ are moving with velocities $$2\,m/s$$ and $$10\,m/s$$ respectively along same direction. Then the velocity of their centre of mass will be
A
$$8.1\,m/s$$
B
$$7.3\,m/s$$
C
$$6.4\,m/s$$
D
$$5.3\,m/s$$
Answer :
$$7.3\,m/s$$
210. A circular disc is to be made using iron and aluminium. To keep its moment of inertia maximum about a geometrical axis, it should be so prepared that
A
aluminium is at the interior and iron surrounds it
B
iron is at the interior and aluminium surrounds it
C
aluminium and iron layers are in alternate order
D
sheet of iron is used at both external surfaces and aluminium sheet as inner material
Answer :
aluminium is at the interior and iron surrounds it