181. Two persons of masses $$55\,kg$$ and $$65\,kg$$ respectively, are at the opposite ends of a boat. The length of the boat is $$3.0\,m$$ and weighs $$100\,kg.$$ The $$55\,kg$$ man walks up to the $$65\,kg$$ man and sits with him. If the boat is in still water the centre of mass of the system shifts by :
A
$$3.0\,m$$
B
$$2.3\,m$$
C
zero
D
$$0.75\,m$$
Answer :
zero
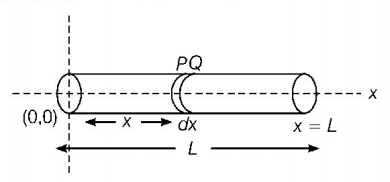
182. A rod is of length $$3\,m$$ and its mass acting per unit length is directly proportional to distance $$x$$ from its one end. The centre of gravity of the rod from that end will be at
A
$$1.5\,m$$
B
$$2\,m$$
C
$$2.5\,m$$
D
$$3\,m$$
Answer :
$$1.5\,m$$
183. Four identical thin rods each of mass $$M$$ and length $$l,$$ form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is :
A
$$\frac{2}{3}M{l^2}$$
B
$$\frac{{13}}{3}M{l^2}$$
C
$$\frac{1}{3}M{l^2}$$
D
$$\frac{4}{3}M{l^2}$$
Answer :
$$\frac{4}{3}M{l^2}$$
184. A solid cylinder of mass $$50\,kg$$ and radius $$0.5\,m$$ is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of $$2\,rev/{s^2}$$ is
A
$$25\,N$$
B
$$50\,N$$
C
$$78.5\,N$$
D
$$157\,N$$
Answer :
$$157\,N$$
185. The free end of a thread wound on a bobbin is passed round a nail $$A$$ hammered into the wall. The thread is pulled at a constant velocity. Assuming pure rolling of bobbin, find the velocity $${v_0}$$ of the centre of the bobbin at the instant when the thread forms an angle $$\alpha $$ with the vertical.
A
$$\frac{{vR}}{{R\sin \alpha - r}}$$
B
$$\frac{{vR}}{{R\sin \alpha + r}}$$
C
$$\frac{{2vR}}{{R\sin \alpha + r}}$$
D
$$\frac{v}{{R\sin \alpha + r}}$$
Answer :
$$\frac{{vR}}{{R\sin \alpha - r}}$$
186. A hoop of radius $$r$$ and mass $$m$$ rotating with an angular velocity $${\omega _0}$$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?
A
$$\frac{{r{\omega _0}}}{4}$$
B
$$\frac{{r{\omega _0}}}{3}$$
C
$$\frac{{r{\omega _0}}}{2}$$
D
$$r{\omega _0}$$
Answer :
$$\frac{{r{\omega _0}}}{2}$$
187.
$$O$$ is the centre of an equilateral $$\Delta ABC.$$ $${F_1},{F_2}$$ and $${F_3}$$ are three forces acting along the sides $$AB,\,BC$$ and $$AC$$ as shown in figure. What should be the magnitude of $${F_3},$$ so that the total torque about $$O$$ is zero?

A
$$\frac{{\left( {{F_1} + {F_2}} \right)}}{2}$$
B
$$\left( {{F_1} - {F_2}} \right)$$
C
$$\left( {{F_1} + {F_2}} \right)$$
D
$$2\left( {{F_1} + {F_2}} \right)$$
Answer :
$$\left( {{F_1} + {F_2}} \right)$$
188.
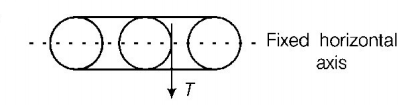
Seven identical circular planar disks, each of mass $$M$$ and radius $$R$$ are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point $$P$$ is:

A
$$\frac{{19}}{2}M{R^2}$$
B
$$\frac{{55}}{2}M{R^2}$$
C
$$\frac{{73}}{2}M{R^2}$$
D
$$\frac{{181}}{2}M{R^2}$$
Answer :
$$\frac{{181}}{2}M{R^2}$$
189. A thin circular ring of mass $$M$$ and radius $$R$$ is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity $$\omega .$$ If two objects each of mass $$m$$ be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
A
$$\frac{{\omega \left( {M - 2m} \right)}}{{M + 2m}}$$
B
$$\frac{{\omega M}}{{M + 2m}}$$
C
$$\frac{{\omega \left( {M + 2m} \right)}}{M}$$
D
$$\frac{{\omega M}}{{M + m}}$$
Answer :
$$\frac{{\omega M}}{{M + 2m}}$$
190. A ring of mass $$m$$ and radius $$r$$ rotates about an axis passing through its centre and perpendicular to its plane with angular velocity $$\omega .$$ Its kinetic energy is
A
$$\frac{1}{2}m{r^2}{\omega ^2}$$
B
$$mr{\omega ^2}$$
C
$$m{r^2}{\omega ^2}$$
D
$$\frac{1}{3}m{r^2}{\omega ^2}$$
Answer :
$$\frac{1}{2}m{r^2}{\omega ^2}$$