11. A wheel having angular momentum $$2\pi \,kg - {m^2}/s$$ about its vertical axis, rotates at the rate of $$60\,rpm$$ about this axis, The torque which can stop the wheel’s rotation in $$30\,\sec$$ would be
A
$$\frac{\pi }{{18}}Nm$$
B
$$\frac{{2\pi }}{{15}}Nm$$
C
$$\frac{\pi }{{12}}Nm$$
D
$$\frac{\pi }{{15}}Nm$$
Answer :
$$\frac{\pi }{{15}}Nm$$
12. Four identical thin rods each of mass $$M$$ and length $$l,$$ form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
A
$$\frac{4}{3}M{l^2}$$
B
$$\frac{2}{3}M{l^2}$$
C
$$\frac{{13}}{3}M{l^2}$$
D
$$\frac{1}{3}M{l^2}$$
Answer :
$$\frac{4}{3}M{l^2}$$
13. A body $$A$$ of mass $$M$$ while falling vertically downwards under gravity breaks into two parts; a body $$B$$ of mass $$\frac{1}{3}M$$ and a body $$C$$ of mass $$\frac{2}{3}M.$$ The centre of mass of bodies $$B$$ and $$C$$ taken together shifts compared to that of body $$A$$
A
does not shift
B
depends on height of breaking
C
towards body $$B$$
D
towards body $$C$$
Answer :
does not shift
14. A cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the frictional force acting on the cylinder are-
A
up the incline while ascending and down the incline descending
B
up the incline while ascending as well as descending
C
down the incline while ascending and up the incline while descending
D
down the incline while ascending as well as descending
Answer :
up the incline while ascending as well as descending
15. Consider a two particle system with particles having masses $${m_1}$$ and $${m_2}.$$ If the first particle is pushed towards the centre of mass through a distance $$d,$$ by what distance should the second particle is moved, so as to keep the centre of mass at the same position?
A
$$\frac{{{m_2}}}{{{m_1}}}d$$
B
$$\frac{{{m_1}}}{{{m_1} + {m_2}}}d$$
C
$$\frac{{{m_1}}}{{{m_2}}}d$$
D
$$d$$
Answer :
$$\frac{{{m_1}}}{{{m_2}}}d$$
16. Moment of inertia of a uniform circular disc about a diameter is $$I.$$ Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be
A
$$5I$$
B
$$3I$$
C
$$6I$$
D
$$4I$$
Answer :
$$6I$$
17. A cart of mass $$M$$ is tied to one end of a massless rope of length $$10\,m.$$ The other end of the rope is in the hands of a man of mass $$M.$$ The entire system is on a smooth horizontal surface. The man is at $$x = 0$$ and the cart at $$x = 10\,m.$$ If the man pulls the cart by the rope, the man and the cart will meet at the point
A
they will never meet
B
$$x = 10\,m$$
C
$$x = 5\,m$$
D
$$x = 0$$
Answer :
$$x = 5\,m$$
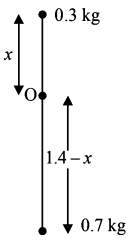
18. Two point masses of $$0.3 \,kg$$ and $$0.7 \,kg$$ are fixed at the ends of a rod of length $$1.4 \,m$$ and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of-
A
$$0.42 \,m$$ from mass of $$0.3 \,kg$$
B
$$0.70 \,m$$ from mass of $$0.7 \,kg$$
C
$$0.98 \,m$$ from mass of $$0.3 \,kg$$
D
$$0.98 \,m$$ from mass of $$0.7 \,kg$$
Answer :
$$0.98 \,m$$ from mass of $$0.3 \,kg$$
19.
One solid sphere $$A$$ and another hollow sphere $$B$$ are of same mass and same outer radii, Their moments of inertia about their diameters are respectively $${I_A}$$ and $${I_B},$$ such that
Here $${\rho _A}$$ and $${\rho _B}$$ represent their densities.
A
$${I_A} = {I_B}$$
B
$${I_A} > {I_B}$$
C
$${I_A} < {I_B}$$
D
$$\frac{{{I_A}}}{{{I_B}}} = {\rho _A} = {\rho _B}$$
Answer :
$${I_A} < {I_B}$$
20. Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities $${\omega _1}$$ and $${\omega _2}.$$ They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is
A
$$\frac{1}{2}I{\left( {{\omega _1} + {\omega _2}} \right)^2}$$
B
$$\frac{1}{4}I{\left( {{\omega _1} - {\omega _2}} \right)^2}$$
C
$$I{\left( {{\omega _1} - {\omega _2}} \right)^2}$$
D
$$\frac{1}{8}{\left( {{\omega _1} - {\omega _2}} \right)^2}$$
Answer :
$$\frac{1}{4}I{\left( {{\omega _1} - {\omega _2}} \right)^2}$$
.PNG)