171.
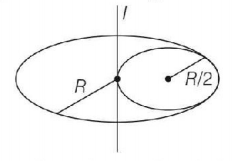
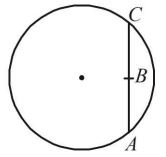
A thin wire of length $$L$$ and uniform linear mass density $$\rho $$ is bent into a circular loop with centre at $$O$$ as shown. The moment of inertia of the loop about the axis $$XX’$$ is
A
$$\frac{{\rho {L^3}}}{{8{\pi ^2}}}$$
B
$$\frac{{\rho {L^3}}}{{16{\pi ^2}}}$$
C
$$\frac{{5\rho {L^3}}}{{16{\pi ^2}}}$$
D
$$\frac{{3\rho {L^3}}}{{8{\pi ^2}}}$$
Answer :
$$\frac{{3\rho {L^3}}}{{8{\pi ^2}}}$$
172. From a disc of radius $$R$$ and mass $$M,$$ a circular hole of diameter $$R,$$ whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
A
$$\frac{{13\,M{R^2}}}{{32}}$$
B
$$\frac{{11\,M{R^2}}}{{32}}$$
C
$$\frac{{9\,M{R^2}}}{{32}}$$
D
$$\frac{{15\,M{R^2}}}{{32}}$$
Answer :
$$\frac{{13\,M{R^2}}}{{32}}$$
173. When a mass is rotating in a plane about a fixed point, its angular momentum is directed along
A
a line perpendicular to the plane of rotation
B
the line making an angle of $${45^ \circ }$$ to the plane of rotation
C
the radius
D
the tangent to the orbit
Answer :
a line perpendicular to the plane of rotation
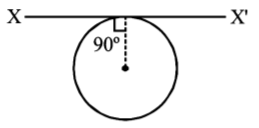
174.
The moment of inertia of a uniform circular disc (figure) is maximum about an axis perpendicular to the disc and passing through
A
$$B$$
B
$$C$$
C
$$D$$
D
$$A$$
Answer :
$$B$$
175. From a solid sphere of mass $$M$$ and radius $$R$$ a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its center and perpendicular to one of its faces is:
A
$$\frac{{4M{R^2}}}{{9\sqrt 3 \pi }}$$
B
$$\frac{{4M{R^2}}}{{3\sqrt 3 \pi }}$$
C
$$\frac{{M{R^2}}}{{32\sqrt 2 \pi }}$$
D
$$\frac{{M{R^2}}}{{16\sqrt 2 \pi }}$$
Answer :
$$\frac{{4M{R^2}}}{{9\sqrt 3 \pi }}$$
176.
$$ABC$$ is a right angled triangular plate of uniform thickness. The sides are such that $$AB > BC$$ as shown in figure. $${I_1},{I_1},{I_3}$$ are moments of inertia about $$AB,\,BC$$ and $$AC$$ respectively. Then, which of the following relations is correct?
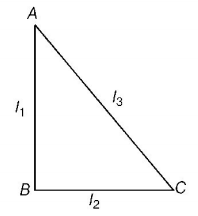
A
$${I_1} = {I_1} = {I_3}$$
B
$${I_2} > {I_1} > {I_3}$$
C
$${I_3} < {I_2} < {I_1}$$
D
$${I_3} > {I_1} > {I_2}$$
Answer :
$${I_2} > {I_1} > {I_3}$$
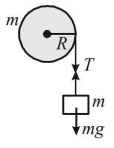
177. A mass $$m$$ hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass $$m$$ and radius $$R.$$ Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass $$m,$$ if the string does not slip on the pulley, is:
A
$$g$$
B
$$\frac{2}{3}g$$
C
$$\frac{g}{3}$$
D
$$\frac{3}{2}g$$
Answer :
$$\frac{2}{3}g$$
178.
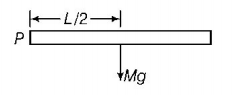
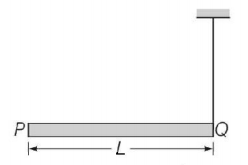
A rod $$PQ$$ of mass $$M$$ and length $$L$$ is hinged at end $$P.$$ The rod is kept horizontal by a massless string tied to a point $$Q$$ as shown in figure. When string is cut, the initial angular acceleration of the rod is
A
$$\frac{{3g}}{{2L}}$$
B
$$\frac{g}{L}$$
C
$$\frac{{2g}}{L}$$
D
$$\frac{{2g}}{{3L}}$$
Answer :
$$\frac{{3g}}{{2L}}$$
179. If $${I_{xy}}$$ is the moment of inertia of a ring about a tangent in the plane of the ring and $${I_{x'y'}}$$ is the moment of inertia of a ring about a tangent perpendicular to the plane of the ring then
A
$${I_{xy}} = {I_{x'y'}}$$
B
$${I_{xy}} = \frac{1}{2}{I_{x'y'}}$$
C
$${I_{x'y'}} = \frac{3}{4}{I_{xy}}$$
D
$${I_{xy}} = \frac{3}{4}{I_{x'y'}}$$
Answer :
$${I_{xy}} = \frac{3}{4}{I_{x'y'}}$$
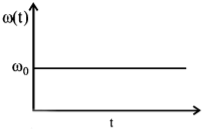
180. A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity $${\omega _0}.$$ When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform $$\omega \left( t \right)$$ will vary with time $$t$$ as-
A

B
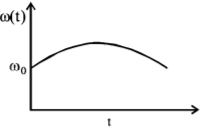

C
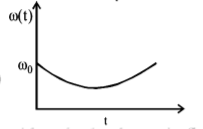

D
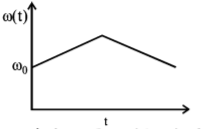

Answer :