141. A couple produces
A
no motion
B
linear and rotational motion
C
purely rotational motion
D
purely linear motion
Answer :
purely rotational motion
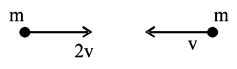
142. Two identical particles move towards each other with velocity $$2v$$ and $$v$$ respectively. The velocity of centre of mass is-
A
$$v$$
B
$$\frac{v}{3}$$
C
$$\frac{v}{2}$$
D
$$Zero$$
Answer :
$$\frac{v}{2}$$
143. A mass is revolving in a circle which is in the plane of paper. The direction of angular acceleration is
A
upward the radius
B
towards the radius
C
tangential
D
at right angle to angular velocity
Answer :
upward the radius
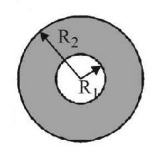
144. The moment of inertia of a hollow thick spherical shell of mass $$M$$ and its inner radius $${R_1}$$ and outer radius $${R_2}$$ about its diameter is
A
$$\frac{{2M}}{5}\frac{{\left( {R_2^5 - R_1^5} \right)}}{{\left( {R_2^3 - R_1^3} \right)}}$$
B
$$\frac{{2M}}{3}\frac{{\left( {R_2^5 - R_1^5} \right)}}{{\left( {R_2^3 - R_1^3} \right)}}$$
C
$$\frac{{4M}}{5}\frac{{\left( {R_2^5 - R_1^5} \right)}}{{\left( {R_2^3 - R_1^3} \right)}}$$
D
$$\frac{{4M}}{3}\frac{{\left( {R_2^5 - R_1^5} \right)}}{{\left( {R_2^3 - R_1^3} \right)}}$$
Answer :
$$\frac{{2M}}{5}\frac{{\left( {R_2^5 - R_1^5} \right)}}{{\left( {R_2^3 - R_1^3} \right)}}$$
145. A cylinder of height $$20 \,m$$ is completely filled with water. The velocity of efflux of water $$\left( {{\text{in m}}{{\text{s}}^{ - 1}}} \right)$$ through a small hole on the side wall of the cylinder near its bottom is-
A
10
B
20
C
25.5
D
5
Answer :
20
146. Two persons of masses $$55\,kg$$ and $$65\,kg$$ respectively, are at the opposite ends of a boat. The length of the boat is $$3\,m$$ and weighs $$100\,kg.$$ The $$55\,kg$$ man walks upto the $$65\,kg$$ man and sits with him. If the boat is in still water the centre of mass of the system shifts by
A
$$3\,m$$
B
$$2.3\,m$$
C
zero
D
$$0.75\,m$$
Answer :
zero
147. A thin rod of length $$L$$ and mass $$M$$ is bent at its mid-point into two halves so that the angle between them is $${90^ \circ }.$$ The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is
A
$$\frac{{M{L^2}}}{{24}}$$
B
$$\frac{{M{L^2}}}{{12}}$$
C
$$\frac{{M{L^2}}}{6}$$
D
$$\frac{{\sqrt 2 M{L^2}}}{{24}}$$
Answer :
$$\frac{{M{L^2}}}{{12}}$$
148. A solid sphere of radius $$R$$ is placed on a smooth horizontal surface. A horizontal force $$F$$ is applied at height $$h$$ from the lowest point. For the maximum acceleration of the centre of mass,
A
$$h = R$$
B
$$h = 2R$$
C
$$h = 0$$
D
The acceleration will be same whatever $$h$$ may be
Answer :
The acceleration will be same whatever $$h$$ may be
149.
One quarter sector is cut from a uniform circular disc of radius $$R.$$ This sector has mass $$M.$$ It is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is
A
$$\frac{1}{2}M{R^2}$$
B
$$\frac{1}{4}M{R^2}$$
C
$$\frac{1}{8}M{R^2}$$
D
$$\sqrt 2 M{R^2}$$
Answer :
$$\frac{1}{2}M{R^2}$$
150. The ratio of the radii of gyration of a circular disc to that of a circular ring, each of same mass and radius, around their respective axes is
A
$$\sqrt 3 :\sqrt 2 $$
B
$$1:\sqrt 2 $$
C
$$\sqrt 2 :1$$
D
$$\sqrt 2 :\sqrt 3 $$
Answer :
$$1:\sqrt 2 $$